SENSITIVITY ANALYSIS ON FACTORS INFLUENCING LANDSLIDE STABILITY AND DISCUSSION ON ITS TREATMENT DESIGN
-
摘要: 对一给定的滑坡(即滑坡坡率、坡高等已确定), 稳定系数的影响因素有滑带土粘聚力、内摩擦角、滑体容重和孔隙水压力等。由于各因素对稳定系数的影响程度不同(即敏感性大小不同), 因此, 需要以定量的标准来找出其中影响较大的因子, 作为滑坡治理重点研究的对象, 有效提高滑坡整治效果。本文以延安市宝塔区王良寺滑坡为例, 采用正交分析法对滑坡稳定性的影响因子进行了分析, 并计算出各种组合的滑坡稳定系数, 然后采用极差分析对因子进行敏感性评价; 以分析结果为基础, 提出滑坡的治理方案, 以期达到经济合理的治理效果。Abstract: The factors influencing landslide stability coefficients include cohesion of soil in the slide zone, internal friction angle, unit weight of the slide and the pore water pressure, etc.They affect the lan dslide stability coefficients in different degrees, so that one imposing the greatest influence on the lan dslide stability coefficients needs to be recognized by quantitative criteria, and studied more closely, to improve treatment effect.In this paper, all the factors are analyzed by using orthogonal analysis method, and various landslide stability coefficients calculated, which is thought helpful to reaching a reasonable and economic treatment.
-
Key words:
- landslide /
- stability /
- orthogonality analysis method /
- sensitivity analysis /
- treatment
-
0. 引言
影响滑坡稳定的因素较多, 且各因素存在复杂性及不确定性, 目前对其研究大多从地形地貌、岩土体性质、岩土体结构面、地下水、地震、工程影响等方面进行分析评价[1~2]。在一定的滑坡工程地质条件下, 有些因素对滑坡失稳影响较大, 而有些则较小, 这就是说, 影响因素对滑坡失稳的贡献是不同的。
滑坡稳定影响因素的敏感性分析就是定量分析影响滑坡稳定性的各因素与滑坡稳定系数之间的相关性, 即分析各因素的变化对于滑坡稳定系数的影响。分析滑坡影响因素的变化与滑坡稳定性的相关关系以及滑坡在不同外界条件下的稳定性, 不但可以找出滑坡失稳的主导因素, 而且根据敏感性分析得出的主要影响因素, 在滑坡治理及优化设计中就可以有针对性的采取相应的整治措施, 使滑坡治理达到安全、经济和有效的目的。因此, 在滑坡及滑坡治理工程中, 影响因素的敏感性分析显得非常重要。
1. 王良寺滑坡概况及其工程地质条件[3]
1.1 滑坡工程概况
王良寺滑坡位于延安市宝塔区桥沟镇东十里铺村, 延河河谷北岸山坡上, 西距延安市中心延河大桥约5.5km, 东临延安飞机场, 南约1km为210国道。
该滑波在延安市宝塔区政府修建的经济适用房场区———又称窑洞小区。窑洞小区投资2亿多元, 共分三期, 其中第一期已交付使用, 在建的第二期工程顺坡台阶式展布, 共六排四列, 多为跃层式别墅房, 少者两层半, 多者四层半, 占地面积100余亩。据现场勘察和走访调查, 第二期工程场地位于一老滑坡体(即王良寺滑坡)上, 其滑坡体体积超过100 × 104m3, 按滑坡规模和物质组成划分, 该滑坡属于大型黄土滑坡。在平场切坡开挖前是稳定的高陡滑坡, 由于第二期工程的大量开挖活动的影响, 改变了滑坡的应力分布, 使滑坡失稳破坏。
1.2 滑坡工程地质条件
1.2.1 地形地貌
滑坡区地貌单元属黄土梁峁斜坡区, 总体由西北向东南延河河谷倾斜, 平均坡降约20.5 %。
1.2.2 地层岩性
根据工程地质测绘及钻探资料, 滑坡岩土体自上而下共分为两个岩土层, 对其特征分述如下:
① 层新黄土(Q3eol):厚15~25m, 滑坡体的主要组成部分, 土质较均, 岩性为粉质粘土, 褐黄~黄褐色, 硬塑~坚硬, 分布有棕褐色古土壤条带, 多含有钙质结核, 直径3~8cm, 局部呈富集状, 孔隙不发育。
② 层老黄土(Q1-2eol):厚20~25m, 多呈黄褐色, 土质均一, 可塑~硬塑, 针状孔隙发育, 含较多钙质结核, 夹杂有棕褐色古土壤层。
1.2.3 水文地质条件
据钻探及井探资料显示, 滑坡区为贫水区, 地下水位埋深较大, 在滑体前缘的井探中发现地下水(据地面8m)。由此可见, 坡体大部分在地下水位以上。地下水主要接受大气降水补给, 以径流方式向延河排泄。
2. 滑坡稳定敏感性分析的计算方法[3]
敏感性分析是系统分析中分析系统稳定的一种方法。对于滑坡系统, 敏感性分析可转化为以滑坡稳定系数FS为考察对象的单指标多因素的显著性分析。本文分析拟采用正交分析法。
单指标多因素的显著性分析可采用线性模型如下:

(1) 式中:β0为常数项; βi为自变量Xi的回归系数; e为随机误差, 服从标准正态分布。
如果在模型中令某些因素的主效应或交互效应为零, 而其余效应的最小二乘估计不受影响, 即与在不假定上述效应为零时所得的估计一致。这保证对每个效应的估计不受到其它效应的影响。则设计矩阵X必须满足如下条件:

(2) 式中:S11、S22、…、Srr都是方阵, 每一块相应于一组效应。
对于某个因素变量Xi对指标Y的显著性次序分析, 不要求做定量结论, 只要求辨明自变量Xi对因变量Y的显著性影响次序。因此无须求解(1)式中的回归系数, 只需按式(2)对各影响因素进行试验设计。此时, 正交试验可满足模型要求。
设A、B、…表示不同的因素; r为各因素水平数; Ai表示因素A的第i水平(i =1, 2, L, r); Xij表示因素j的第i水平的值(i =1, 2, L, r; j =A, B, L)。
在Xij下进行试验得到因素j第i水平的试验结果指标Yij, Yij是服从正态分布的随机变量。在Xij下做了n次试验得到n个试验结果, 分别为Yijk (k =1, 2, L, n)。有计算参数如下:

(3) 式中:Kij为因素j在i水平下的统计参数; n为因素j在i水平下的试验次数; Yijk为因素j在i水平下第k个试验结果指标值。
评价因素显著性的参数为极差Rj, 其计算公式如下:

(4) 极差越大说明该因素的水平改变对试验结果影响也越大。极差最大的因素也就是最主要的因素, 极差较小的因素为较次要的因素, 依此类推。
利用正交分析法可以解决以下几个问题:
(1) 分清各因素对指标影响的主次顺序, 即分清哪些是主要因素, 哪些是次要因素;
(2) 找出优化的设计方案, 即考察的每个因素各取什么水平才能达到试验指标的要求;
(3) 分析因素与指标间的关系, 即当因素变化时指标是怎样变化的, 找出指标随因素的变化规律和趋势。
3. 滑坡稳定敏感性分析
3.1 正交试验设计
王良寺滑坡稳定系数的计算, 采用圆弧条分法中的简化Bishop法[4]。在对其进行正交试验设计时, 考虑的因素主要有粘聚力(c)、内摩擦角(φ)、重度(γ)、地下水位(hw)、坡高(h)等5种参数变化。各影响因素分析均只考虑土体参数的自相关性, 不考虑其的互相关性影响。为了减少由于水平次序引起的系统误差, 各因素水平的次序应随机排列。参数取值范围和按抽签方式确定的因素水平次序如表 1所示。
表 1 各参数取值范围Table 1. The range of each parameter
假设各因素间无交互作用, 可选5因素正交表安排试验。对于4水平5因素正交试验, 最少试验次数为16次, 记为L16 (45)。
3.2 计算结果分析
选用数理统计L16 (45)正交表[5], 按表 1确定的试验方案, 对王良寺滑坡进行以稳定系数为指标的多因素显著性计算分析。正交试验因素水平概化值及计算结果如表 2所示。
表 2 正交试验计算结果Table 2. Results of orthogonality test
对于因素γ, 它的第一水平(γ=16)下的4次计算(表 2中试验号1, 2, 3, 4)求得的稳定系数之和K1j=3.955;第二水平(γ=18)下的4次计算(试验号5, 6, 7, 8)求得的稳定系数之和K2j =3.825;依此类推, 如表 3。
表 3 不同重度值的稳定性系数Table 3. Stability coefficient of different weights
对于因素c, 它的第一水平(c =57)下的4次计算(表 2中试验号1, 5, 9, 13)求得的稳定系数之和K1 j =4.417;第二水平(c =43)下的4次计算(试验号2, 6, 10, 14)求得的稳定系数之和K2j =3.891;依此类推, 如表 4。
表 4 不同粘聚力的稳定性系数Table 4. Stability coefficient of different cohesive forces
用同样的方法计算φ、h、hw相应的稳定系数之和K1j、K2j、K3j、K4j, 如表 5、表 6、表 7。
表 5 不同内摩擦角的稳定性系数Table 5. Stability coefficient of different internal friction angles 表 6 不同坡高的稳定性系数Table 6. Stability coefficient of different slope heights
表 6 不同坡高的稳定性系数Table 6. Stability coefficient of different slope heights 表 7 不同地下水位的稳定性系数Table 7. Stability coefficient of different groundwater levels
表 7 不同地下水位的稳定性系数Table 7. Stability coefficient of different groundwater levels
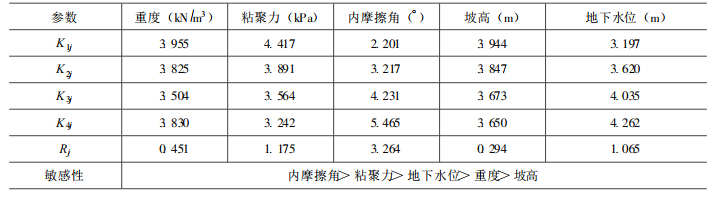
各参数的极差分析如表 8所示。
表 8 各参数极差分析Table 8. Range analysis of parameters
正交试验设计中各因素不同水平之间的搭配是均衡的, 例如根据因素γ的4种不同水平分成的4组计算的每一组计算中, c、φ等其他因素的不同水平皆出现一次。因此γ的K1j、K2j、K3j、K4j之间的差异可以认为主要是γ取不同水平造成的。同理, 哪个因素的极差R大, 就可以认为该因素水平不同对滑坡稳定性产生的影响就大, 影响最大的因素即最敏感因素。从表 8中的极差值可以看出, φ是最敏感的因素, 其他依次为c、hw、γ、h。
4. 滑坡治理措施探讨
王良寺滑坡为一大型黄土老滑坡因不适当开挖引发复活, 滑坡后部宽约130m, 前部宽约270m, 南北长约350m。坡体中部及前部为拟建的经济适用窑小区, 8排24幢房屋, 建成后将有千余人入住, 依据《建筑边坡工程技术规范》 (GB05330-2002), 其安全等级为Ⅱ级。
根据滑坡稳定影响因子敏感性分析结果, 本工程采用上部截排地表水、滑体后部推力段依势适当削坡、下部抗滑桩支挡三种工程相结合的综合治理措施。抗滑桩位置的选择既考虑坡体的整体稳定又能防止坡体的局部剪出。
4.1 截、排水工程
上部截水沟在滑坡后壁后侧, 依滑坡后壁走势布置, 内截面倒梯形, 长度约400m, 排水沟纵向坡率为3 ‰, 水沟材料采用浆砌片石, 等级为M10。
4.2 削坡、护坡工程
削坡工程充分利用黄土局部直立性能好的特点, 分级削坡, 每级坡高为10m, 坡比为1: 1.5, 共5级, 两级削坡间设3m宽平台。部分削坡土方回填于下部抗滑桩后, 既减少土方运距又可适当压脚。护坡工程采用2m ×2m尺寸的菱形网格格构, 格体采用M10浆砌片石构筑, 截面尺寸为300mm×400mm。
4.3 支挡工程
支挡工程采用半悬臂式抗滑桩。设计中采用的土体力学参数为:滑面以上土体重度γ= 16kN/m3, 粘聚力c =31kPa, 内摩擦角φ=23°; 滑体后部滑动带土体重度γ=18kN/m3, 粘聚力c =25kPa, 内摩擦角φ=18°; 滑面以下土体重度为γ=18kN/m3, 粘聚力c =31kPa, 内摩擦角φ=23°。取边坡稳定安全系数为1.25, 采用圆弧滑动法计算, 滑面以上适当考虑桩前土的抗力作用, 桩后剩余下滑力和桩前土抗力均按矩形分布, 滑面下按弹性地基梁计算, 地基水平抗力系数m=2000kN/m4。设计抗滑桩截面尺寸为2.5m×3.5m, 中至中间距为6m。
5. 结论
采用概率统计原理和计算机电算技术的正交分析法对滑坡稳定影响因子进行敏感性分析, 其工作量小、易于完成, 具有一定的通用性, 对工程技术人员来说是一种较实用的分析方法。实例分析表明, 运用正交分析法得到的结论与一般工程经验相符, 因此该方法具有一定的可靠性。
本文在对滑坡稳定性影响因子进行敏感性分析时, 没有考虑参数的相关性对其稳定性的影响, 在今后的工作可以考虑改进正交分析法以进行因素间有交互作用时的分析。实际上岩土体参数c、φ通常呈负相关性, 考虑参数的相关性可以使稳定性分析模型更接近于工程实际, 提高对滑坡稳定系数的计算精度, 以期达到安全、可靠, 经济、合理的治理效果。
-
表 1 各参数取值范围
Table 1. The range of each parameter
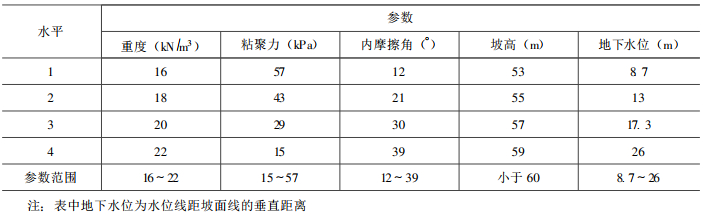
表 2 正交试验计算结果
Table 2. Results of orthogonality test

表 3 不同重度值的稳定性系数
Table 3. Stability coefficient of different weights
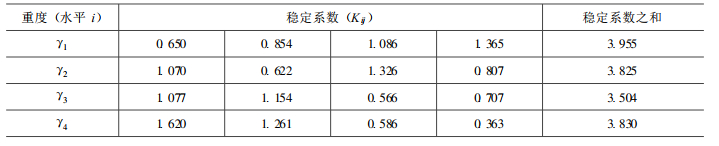
表 4 不同粘聚力的稳定性系数
Table 4. Stability coefficient of different cohesive forces
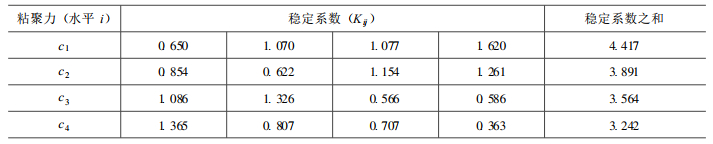
表 5 不同内摩擦角的稳定性系数
Table 5. Stability coefficient of different internal friction angles

表 6 不同坡高的稳定性系数
Table 6. Stability coefficient of different slope heights
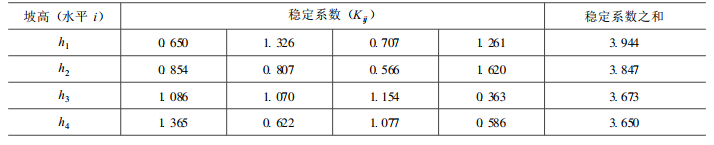
表 7 不同地下水位的稳定性系数
Table 7. Stability coefficient of different groundwater levels
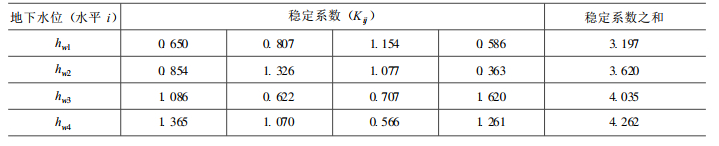
表 8 各参数极差分析
Table 8. Range analysis of parameters
-
[1] 张咸恭, 王思敬, 张倬元, 等.中国工程地质学[M].北京:科学出版社, 2000. [2] Shubh Pathak Bjorn Nilsen.Probabilistic rock slope stability analysis for Himalayan condition[J].Bulletin of Engineering Geology and the Environment, 2004, 63:25~32. doi: 10.1007/s10064-003-0226-1 [3] 张旭辉, 龚晓南, 徐日庆.边坡稳定影响因素敏感性的正交法计算分析[J].中国公路学报, 2003, 16 (1):36 ~39. doi: 10.3321/j.issn:1001-7372.2003.01.009 [4] 钱加欢, 殷宗泽.土工原理与计算[M].北京:中国水利水电出版社, 1996. [5] 侯化国, 王玉民编.正交试验法[M].长春:吉林人民出版社, 1985. -

计量
- 文章访问数: 219
- HTML全文浏览量: 125
- PDF下载量: 9
- 被引次数: 0




 下载:
下载:

 下载:
下载:
