基于水压致裂法的三山岛深竖井工程区地应力测量与反演分析

朱明德; 王照亚; 张月征; 李文光; 侯奎奎; 纪洪广; 尹延天; 付桢; 郝英杰

doi:10.12090/j.issn.1006-6616.20232911

基于水压致裂法的三山岛深竖井工程区地应力测量与反演分析

doi: 10.12090/j.issn.1006-6616.20232911

朱明德^{1, 2,},
王照亚^3, ,,
张月征^{4, 5},
李文光³,
侯奎奎^{1, 2},
纪洪广^{4, 5},
尹延天^{1, 2},
付桢^{4, 5},
郝英杰^{1, 2}

1.
山东黄金集团有限公司深井开采实验室，山东莱州 261400
2.
山东省深海深地金属矿智能开采重点实验室，山东莱州 261400
3.
山东黄金矿业（莱州）有限公司三山岛金矿，山东莱州 261400
4.
北京科技大学城市地下空间工程北京市重点实验室，北京 100083
5.
矿山深井建设技术国家工程研究中心，北京 100013

基金项目: 山东省自然科学基金项目（ZR2021ZD36）

详细信息

作者简介:
朱明德（1988—），男，硕士，主要从事岩石力学与地应力测量等相关工作。E-mail：zhumingde@sd-gold.com

通讯作者:
王照亚（1969—），男，高级工程师，主要从事岩石力学基础理论与岩土工程相关工作。E-mail：wangzhaoya@sd-gold.com

中图分类号: P553
计量
- 文章访问数: 555
- HTML全文浏览量: 111
- PDF下载量: 69
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-28
- 修回日期: 2023-04-25
- 录用日期: 2023-05-08

In-situ stress measurement and inversion analysis of the deep shaft project area in Sanshan Island based on hydraulic fracturing method

ZHU Mingde^{1, 2
,},
WANG Zhaoya^{3
, ,},
ZHANG Yuezheng^{4, 5},
LI Wenguang³,
HOU Kuikui^{1, 2},
JI Hongguang^{4, 5},
YIN Yantian^{1, 2},
FU Zhen^{4, 5},
HAO Yingjie^{1, 2}

1.
Deep Mining Laboratory of Shandong Gold Group Co Ltd, Laizhou 261400, Shandong, China
2.
Shandong Key Laboratory of Deep-sea and Deep-earth Metallic Mineral Intelligent Mining, Laizhou 261400, Shandong, China
3.
Sanshandao Gold Mine of Shandong Gold Mining Industry Co., Ltd., Laizhou 261400, Shandong, China
4.
Beijing Key Laboratory of Urban Underground Space Engineering, University of Science and Technology Beijing, Beijing 100083, China
5.
National Engineering Research Center of Deep Shaft Construction, Beijing 100013, China

Funds: This research is financially supported by the Shandong Provincial Natural Science Foundation（Grant ZR2021ZD36）

摘要

摘要:
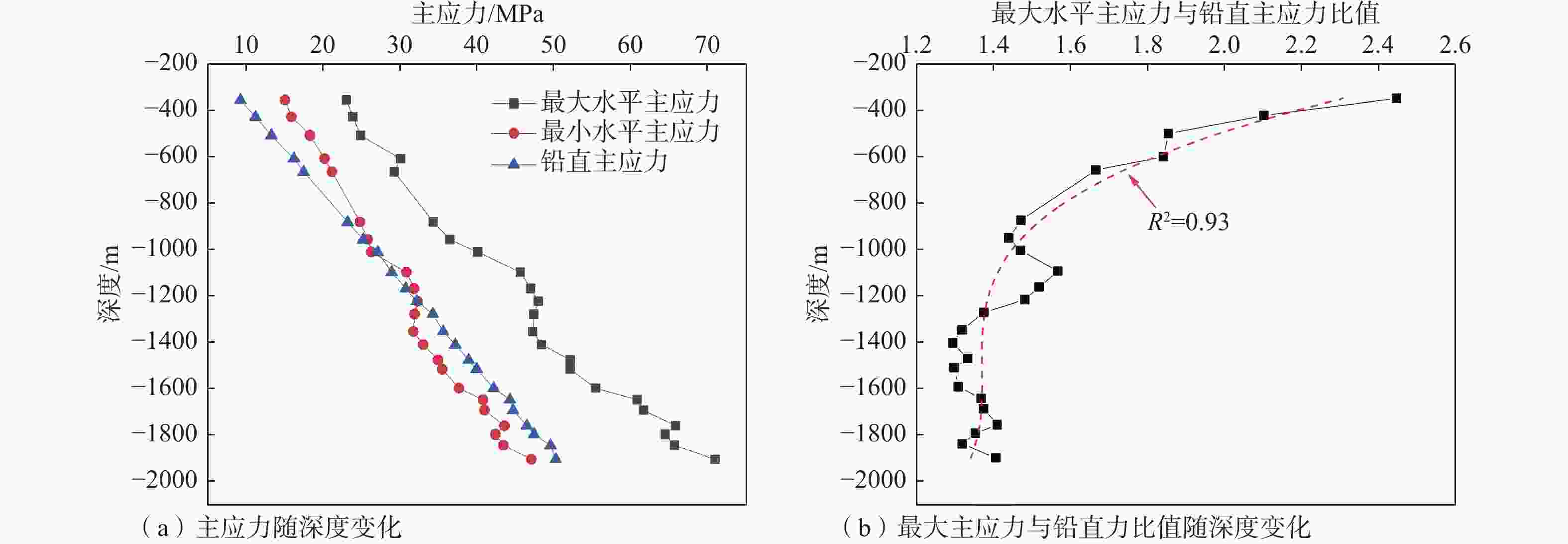
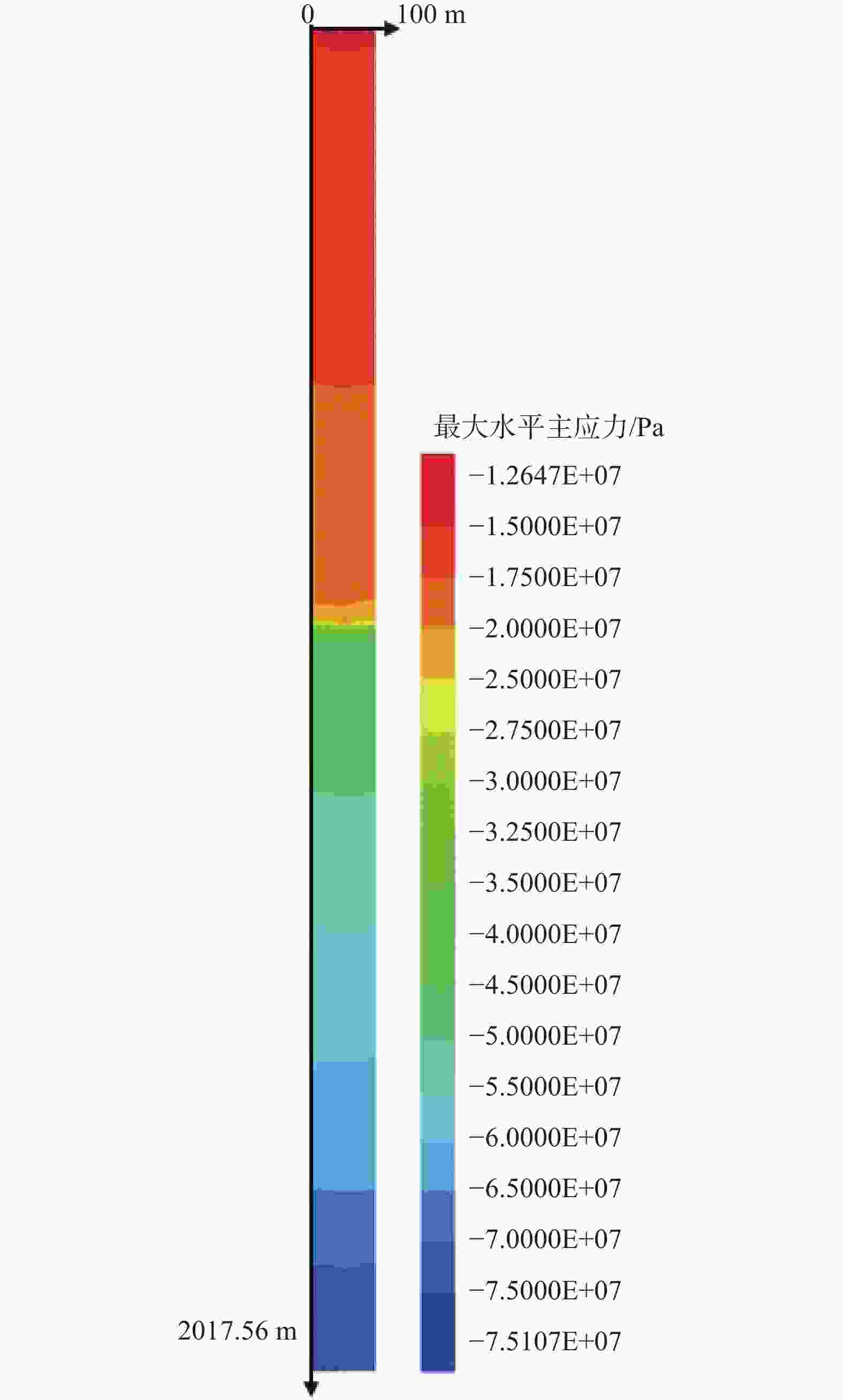
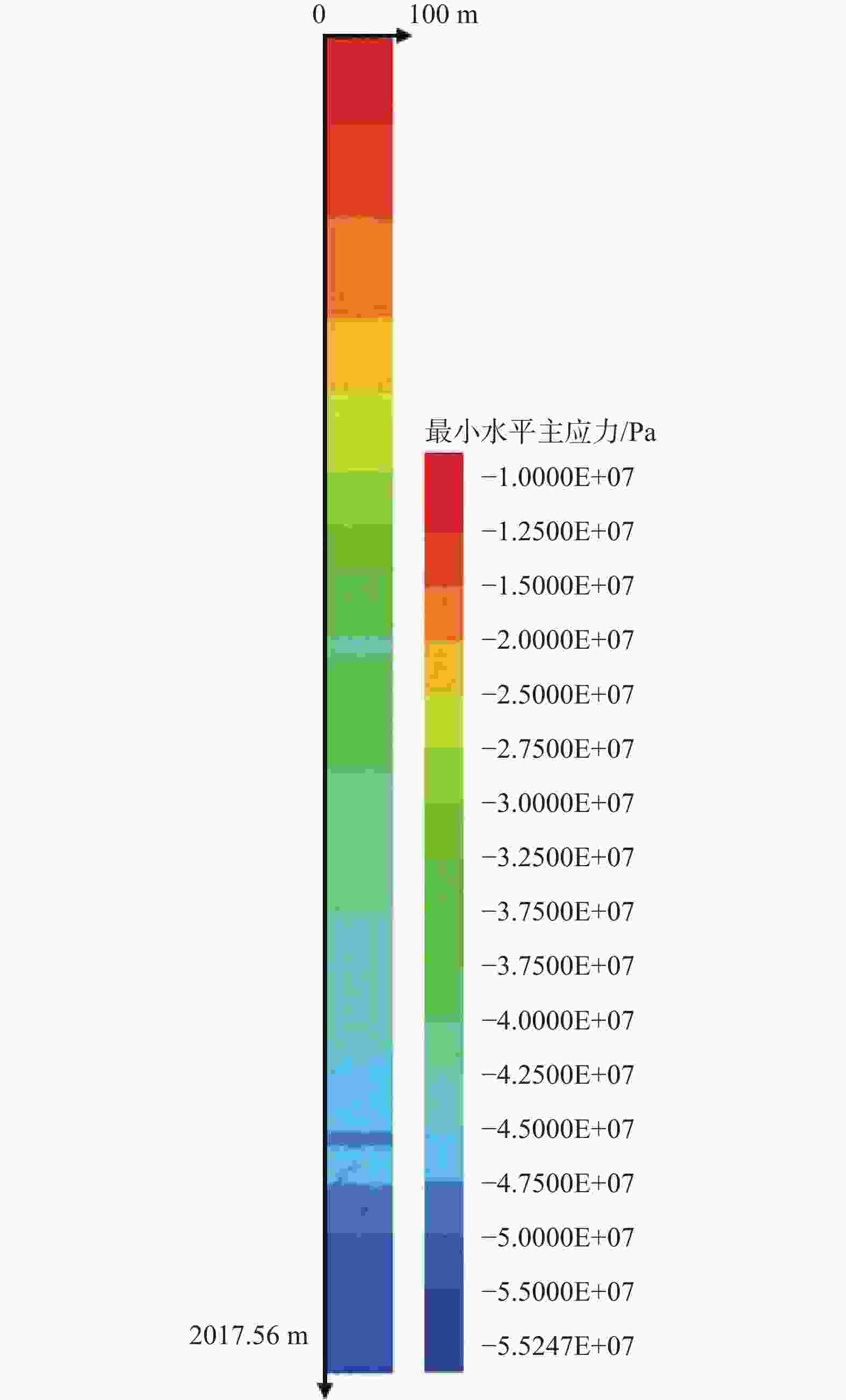
山东省三山岛西岭矿区拟建2000 m深副井，属于超深井建设工程。揭示建井工程区地应力场特征是开展竖井设计、建设施工的必要先决条件之一，研究中采用水压致裂法开展了深部竖井地应力现场测量工作，测量深度达到1899.00 m，通过数值仿真模拟方法反演了竖井工程区2017.56 m深的地应力场。结果表明：在水压致裂测试的钻孔357.76～1899.00 m深度范围内，最大水平主应力（S_H）为23.16～70.86 MPa，最小水平主应力（S_h）为15.24～47.06 MPa；主应力随深度近于线性增加，地应力测量孔实测最大水平主应力方向分别为NW55.5°、NW60.4°、NW58.4°，为近北西方向；竖井工程区应力场主要以水平应力为主导，1200.00 m以下铅直主应力（S_v）为中间应力，S_H与S_v之比平均值为1.53；通过FLAC 3D软件的反演分析获得了建井工程区内地应力场随深度、地层变化的分布规律，测试点的反演结果与实测值基本一致。近2000 m超深地层地应力状态及其分布规律，为竖井工程的井筒井壁设计和工程风险评估提供了基础科学依据。
- 深竖井 /
- 深部地层 /
- 水压致裂法 /
- 地应力测量 /
- 地应力反演
Abstract:
The proposed 2000-meter-deep auxiliary shaft at the Xiling mine, Sanshan Island, Shandong Province, is an ultra-deep shaft construction project. Revealing the characteristics of the in-situ stress field in the shaft construction area is one of the necessary prerequisites for the design and construction of the shaft. We measured the in-situ stress in the deep shaft by hydraulic fracturing method to a depth of 1899.00 m and inverted the 2017.56-meter-deep in-situ stress field in the shaft construction area by numerical simulation. The results show that the maximum horizontal principal stress (S_H) ranges from 23.16 to 70.86 MPa, and the minimum horizontal principal stress (S_h) from 15.24 to 47.06 MPa in the depth range from 357.76 to 1899.00 m in the borehole tested by hydraulic fracturing; the principal stress increases nearly linearly with depth, and the measured maximum horizontal principal stress directions in the measured boreholes are NW 55.5°, NW 60.4°, and NW 58.4°, respectively. Horizontal stress mainly dominates the stress field in the shaft engineering area, the vertical stress (S_v) below 1200.00 m is the intermediate stress, and the average value of the ratio of S_H to S_v is 1.53. The in-situ stress field distribution pattern in the well-construction area with depth and stratigraphic changes is obtained by inversion analysis of FLAC 3D software. The inversion results are basically consistent with the measured values. It provides the fundamental scientific basis for shaft wall design and engineering risk assessment of shaft projects.
- deep shaft /
- deep strata /
- hydraulic fracturing /
- In-situ stress measurement /
- in-situ stress inversion

HTML全文

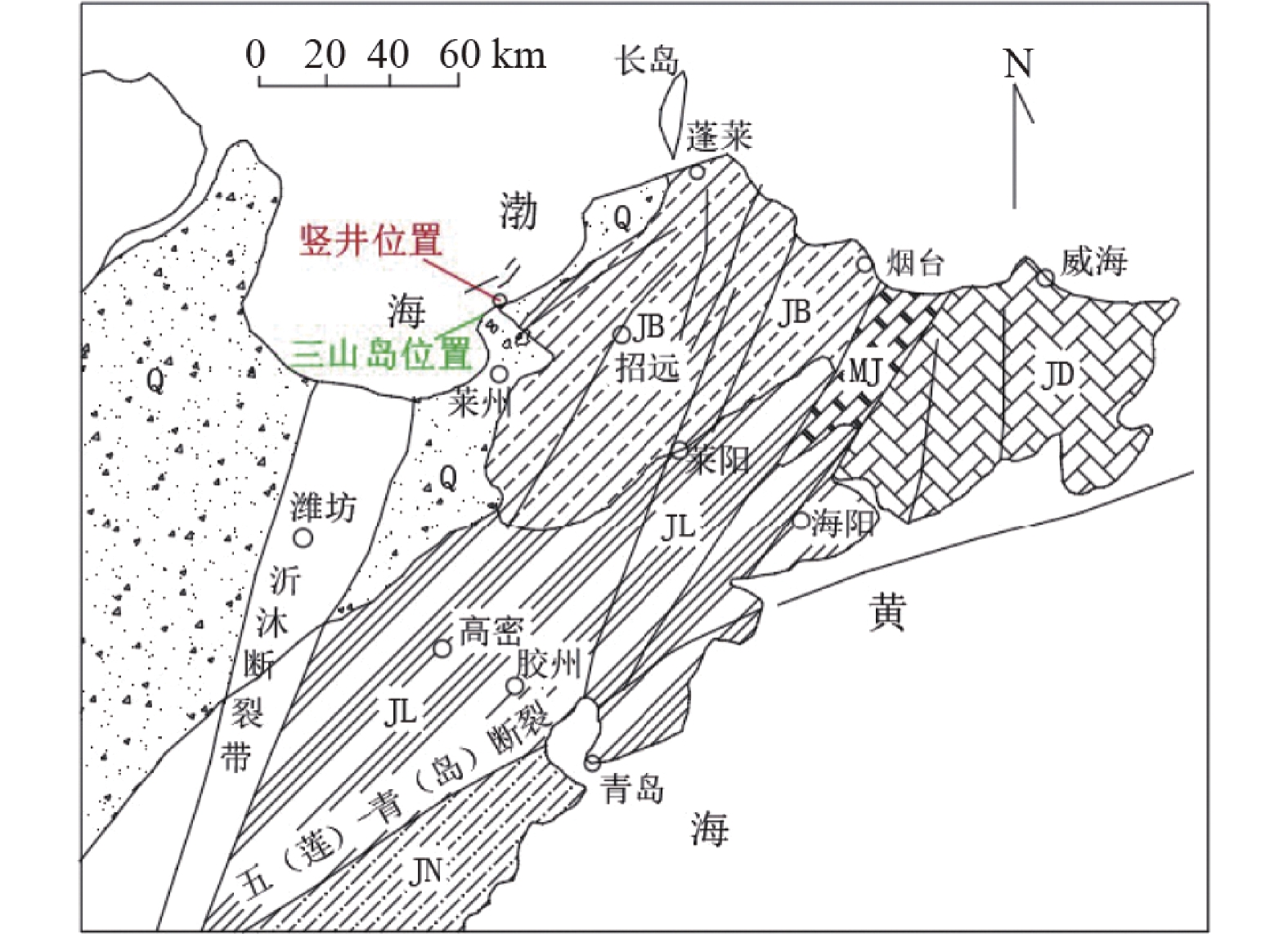
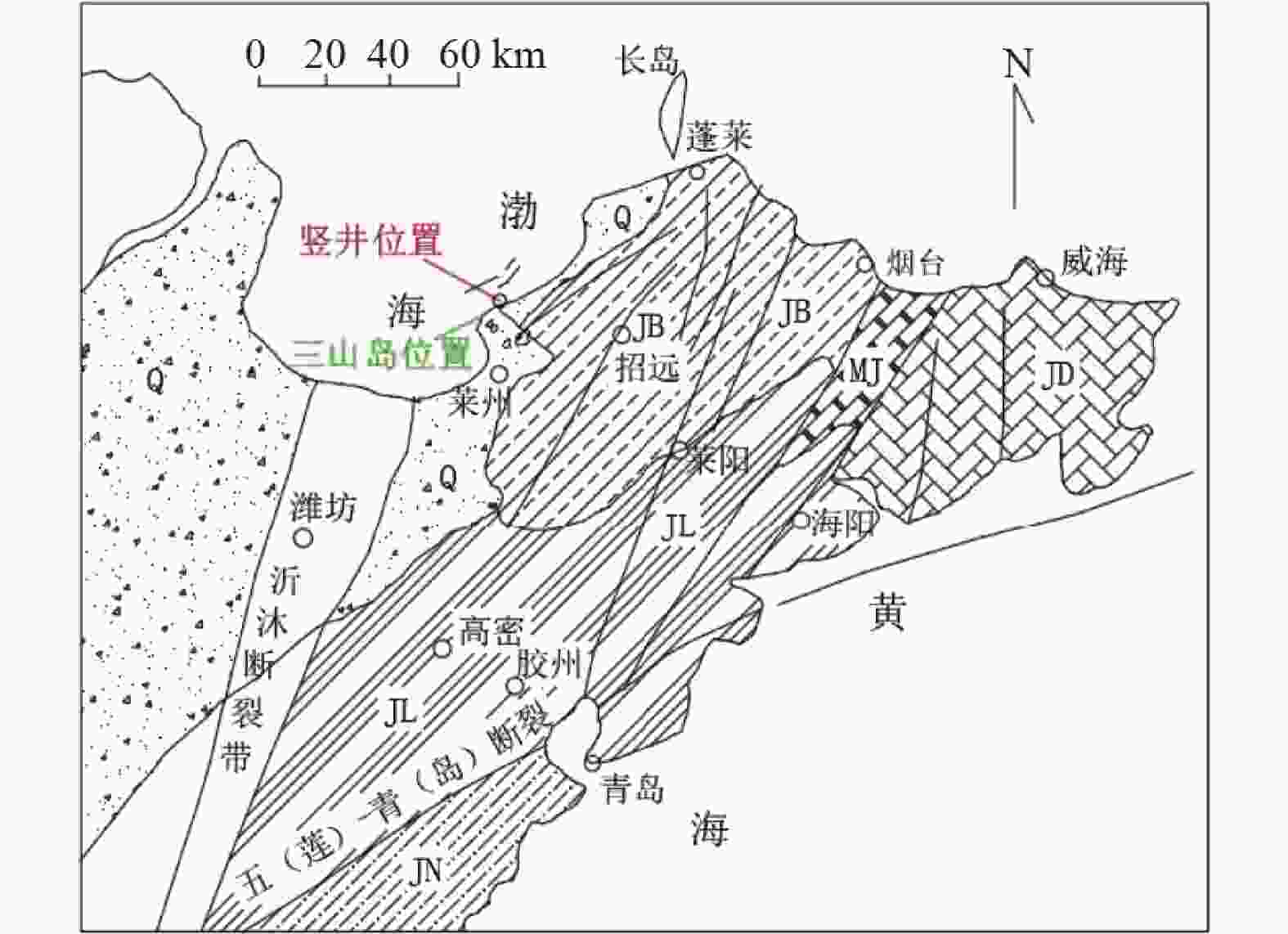
图 1 西岭副井工程地质勘察图

Q—第四系平原区；MJ—牟平−即墨构造混杂带；JD—胶东侵入岩变质区；JB—胶北隆起；JL—胶莱塌陷区；JN—胶南隆起区

Figure 1. Engineering geological map of the Xiling auxiliary shaft

Q−Quaternary plain; MJ−Muping−Jimo tectonic hybrid zone; JD−Jiaodong intrusive metamorphic zone; JB−Jiaobei uplift zone; JL−Jiaolai subsidence zone; JN−Jiaonan uplift zone

下载: 全尺寸图片幻灯片

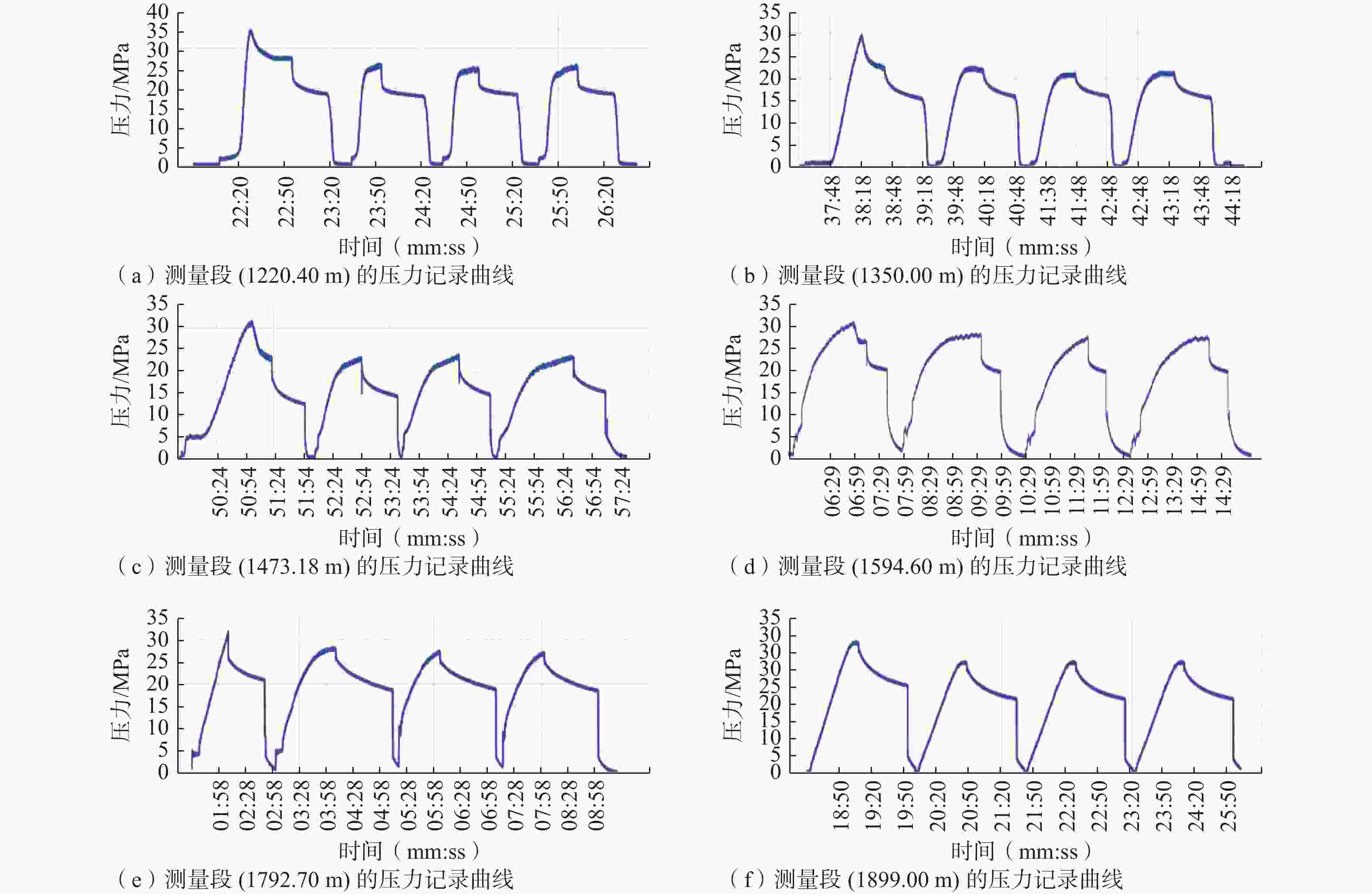
图 2 测量典型压裂过程曲线

1—准备施压阶段；2—施压阶段；3—压裂阶段；4—泄压阶段；5—裂纹闭合阶段；6—重新施压阶段；7—裂隙重新张开阶段；8—重新泄压阶段；9—裂纹闭合阶段

Figure 2. Curves of a typical fracturing process

1–preparation for pressure application; 2–pressure application; 3–fracturing; 4–pressure relief; 5–fracture closure; 6–re-application of pressure; 7–fracture re-opening; 8–re-relief of pressure; 9–fracture closure

下载: 全尺寸图片幻灯片

图 3 单回路水压致裂地应力测量系统

Figure 3. Schematic diagram of the new single-loop hydrofracture in-situ stress measurement system

下载: 全尺寸图片幻灯片

图 4 测量系统的印模装置

Figure 4. Impression devices for measurment system

下载: 全尺寸图片幻灯片

图 5 水压致裂典型压力曲线

Figure 5. Typical curves of hydraulic fracturing pressure

下载: 全尺寸图片幻灯片

图 6 西岭金矿钻孔主应力值随深度变化图与应力关系图

Figure 6. Variation of principal stresses with depth and stress diagram in the Xiling gold deposit

(a) Variation of principal stresses with depth; (b) Ratio of maximum principal stress to vertical stress

下载: 全尺寸图片幻灯片

图 7 地质模型图和网格细节图

Figure 7. Geological model map and grid details

下载: 全尺寸图片幻灯片

图 8 最大水平主应力云图

Figure 8. Cloud of maximum horizontal principal stress

下载: 全尺寸图片幻灯片

图 9 最小水平主应力云图

Figure 9. Cloud of minimum horizontal principal stress

下载: 全尺寸图片幻灯片

图 10 铅直方向主应力云图

Figure 10. Cloud of vertical stress

下载: 全尺寸图片幻灯片

图 11 实测值和理论计算值对比图

Figure 11. Comparison of measured and theoretically calculated values

下载: 全尺寸图片幻灯片

图 12 模型破坏方式模拟分析

Figure 12. Simulation analysis of model damage patterns

下载: 全尺寸图片幻灯片

图 13 深部地应力导致的工程灾害图

Figure 13. Photos of safety issues due to deep in-situ stress

(a) Rock cake-out and fracture; (b) Large deformation in a deep channel

下载: 全尺寸图片幻灯片

表 1 三山岛金矿西岭矿区副井勘察孔水压致裂原地应力测量结果

Table 1. Results of hydraulic fracturing in-situ stress measurements in the borehole of the auxiliary shaft at the Xiling deposit, Sanshandao gold mine

测段深度/m	压裂参数/MPa					主应力值/MPa			破裂方位
测段深度/m	P_b	P_r	P_s	P_o	T	S_H	S_h	S_v	破裂方位
357.76	20.02	15.54	11.73	3.51	4.48	23.16	15.24	9.47
431.09	24.57	15.78	11.85	4.22	8.79	23.99	16.08	11.41
509.35	25.15	20.29	13.44	4.99	4.86	25.02	18.43	13.48	NW55.5°
608.26	25.16	18.82	14.35	5.96	6.34	30.20	20.31	16.39
665.33	24.34	21.39	14.75	6.52	2.95	29.37	21.27	17.60
881.70	30.22	23.09	16.29	8.64	7.14	34.42	24.93	23.33
957.10	25.86	22.54	16.57	9.38	3.33	36.56	25.95	25.32
1010.50	23.06	19.19	16.48	9.90	3.87	40.14	26.38	27.23
1097.50	30.43	25.72	20.19	10.76	4.71	45.62	30.95	29.04	NW60.4°
1166.41	34.84	25.94	20.50	11.43	8.90	46.99	31.93	30.86
1220.40	34.40	25.31	20.44	11.96	9.09	47.96	32.40	32.29
1275.80	32.79	23.63	19.52	12.50	9.16	47.43	32.02	34.38
1350.00	29.30	21.84	18.62	13.23	7.47	47.25	31.85	35.72
1408.00	28.02	23.36	19.32	13.80	4.66	48.40	33.12	37.26
1473.18	31.93	24.09	20.59	14.44	7.85	52.12	35.03	38.98
1512.50	31.01	24.98	20.75	14.82	6.04	52.11	35.58	40.02	NW58.4°
1594.60	31.82	26.59	22.12	15.63	5.23	55.40	37.75	42.19
1643.63	38.98	29.43	24.70	16.11	9.55	60.79	40.81	44.30
1689.50	37.83	28.31	24.46	16.56	9.52	61.63	41.02	44.70
1756.80	34.89	30.65	26.39	17.22	4.24	65.72	43.60	46.48
1792.70	32.69	27.70	24.83	17.57	4.99	64.37	42.40	47.43
1839.00	37.35	28.73	25.43	18.02	8.62	65.58	43.45	49.56
1899.00	42.47	33.10	28.45	18.61	9.37	70.86	47.06	50.25

下载: 导出CSV

表 2 岩石物理力学实验结果统计表

Table 2. Statistics of the physical and mechanical measurements of rocks

采样深度/m	岩性	工程岩组	抗拉强度 σ_t/MPa	抗剪强度（直剪）		弹性模量 E₅₀/×10³ MPa	泊松比 μ₅₀
采样深度/m	岩性	工程岩组	抗拉强度 σ_t/MPa	黏聚力 C/MPa	内摩擦角 φ/（°）	弹性模量 E₅₀/×10³ MPa	泊松比 μ₅₀
4.73～16.93	裂隙较发育，岩芯以碎块、块状为主，部分碎屑状	基岩风化带岩组	1.840			23.300	0.23
			3.980	4.14	43.60	19.700	0.30
			2.300			31.600	0.18
38.00～55.00	裂隙较发育，岩芯以柱状为主，少量碎块	二长花岗岩岩组	6.427	10.43	59.40	3.748	0.11
340.00～400.00			4.914			5.983	0.02
525.00～580.00			4.493	13.00	42.83	7.689	0.27
760.00～800.00			6.049	10.81	58.07	5.302	0.40
935.00～1000.00	裂隙发育，岩芯以柱状、块状、碎块居多，局部小段呈碎屑状	钾化花岗岩岩组	5.350	4.39	53.11	5.500	0.05
1000.00～1050.00	裂隙密集，岩芯以块状、碎块为主	二长花岗岩岩组	5.462	7.82	44.21	4.763	0.21
1050.00～1064.00	裂隙发育，岩芯以块状为主，局部碎块状	绢英岩化花岗岩岩组	6.151	7.89	55.86	3.958	0.24
1140.00～1170.00	裂隙密集，岩芯以块状为主，局部碎块状	二长花岗岩岩组	5.827	3.61	44.58	2.746	0.05
1300.00～1400.00	裂隙密集，岩芯以块状为主，局部碎块状	二长花岗岩岩组	5.305	6.26	45.17	1.837	0.12
1650.00～1700.00	裂隙密集，岩芯以块状、碎块为主	绢英岩化花岗岩岩组	3.251	6.00	36.43	5.165	0.27
1722.96～1728.16	裂隙密集，岩芯以块状、碎块为主	二长花岗岩岩组	3.380	5.17	53.50	21.800	0.20
			4.560			20.500	0.11
			4.820			26.100	0.09
1728.66～1740.46	裂隙密集，岩芯以块状、碎块为主	绢英岩化花岗质碎裂岩岩组	3.940	7.35	54.30	36.200	0.14
			4.990			38.800	0.12
			5.830			46.300	0.05
1740.46～1756.76			7.300	10.54	53.30	43.500	0.09
			6.680			57.300	0.13
			6.530			42.300	0.06
1800.00～1870.00	裂隙密集，岩芯以块状、碎块为主	二长花岗岩岩组	7.360	12.20	53.40	50.500	0.10
			8.310			47.900	0.09
			9.130			48.800	0.03
1960.00～1980.00			7.160	11.47	54.40	59.800	0.07
			8.810			45.400	0.12
			6.710			47.400	0.04
1974.00～1983.00	裂隙发育，岩芯以块状、碎块为主，线裂隙率为10条/米左右	煌斑岩岩组	7.540	14.70	58.30	85.700	0.03
			12.000			92.200	0.09
			9.480			95.200	0.10
1990.00～2000.00	裂隙发育，岩芯以块状、碎块为主	云英岩岩组	7.580	9.54	53.60	52.500	0.11
			5.700			63.800	0.12
			6.160			53.900	0.13
2000.00～2015.00			2.530	2.70	45.20	9.320	0.45
			2.170			11.000	0.34
			2.940			7.950	0.24

下载: 导出CSV

参考文献(63)

[1]	AMADEI B, STEPHANSSON O, 1997. Rock stress and its measurement[M]. Dordrecht: Springer: 95,doi: 10.1007/978-94-011-5346-1.
[2]	CAI M F, 1993. Review of principles and methods for rock stress measurement[J]. Chinese Journal of Rock Mechanics and Engineering, 12(3): 275-283. (in Chinese with English abstract)
[3]	CAI M F, QIAO L, YU B, et al. , 1999. Results and analysis of in-situ stress measurement at deep position of NO. 2 mining area of Jinchuan Nichkel Mine[J]. Chinese Journal of Rock Mechanics and Engineering, 18(4): 414-418,doi: 10.3321/j.issn:1000-6915.1999.04.011. (in Chinese with English abstract)
[4]	CAI M F, 2001. Metal mine design optimization and ground pressure control: theory and practice[M]. Beijing: Science Press: 1-310. (in Chinese)
[5]	CAI M F, CHEN C Z, PENG H, et al. , 2006. In-situ stress measurement by hydraulic fracturing technique in deep position of Wanfu coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 25(5): 1069-1074,doi: 10.3321/j.issn:1000-6915.2006.05.033. (in Chinese with English abstract)
[6]	CHEN Q C, AN M J, LI F Q, 1998. Theoretical discussion on 3-D hydraulic fracturing in situ stress measurement[J]. Journal of Geomechanics, 4(1): 37-44. (in Chinese with English abstract)
[7]	GAI H L, YAO SH H, YANG L P, et al. , 2021. Characteristics and causes of coseismic surface rupture triggered by the “5. 22” M_S 7.4 earthquake in Maduo, Qinghai, and their significance[J]. Journal of Geomechanics, 27(6): 899-912,doi: 10.12090/j.issn.1006-6616.2021.27.06.073. (in Chinese with English abstract)
[8]	GALE W J, BLACKWOOD R L, 1987. Stress distributions and rock failure around coal mine roadways[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 24(3): 165-173,doi: 10.1016/0148-9062(87)90524-9.
[9]	HE M CH, 2004. Present Situation and Prospect of Rock Mechanics in Deep Mining Engineering[C]//Chinese journal of rock mechanics and engineering. Science Press: 99-105. (in Chinese with English abstract)
[10]	HOU K K, WU Q Z, ZHANG F P, et al. , 2022. Application of different in-situ stress test methods in the area of 2 005 m shaft construction of Sanshandao gold mine and distribution law of in-situ stress[J]. Rock and Soil Mechanics, 43(4): 1093-1102,doi: 10.16285/j.rsm.2021.1172. (in Chinese with English abstract)
[11]	JIA C, 2021. Application of hydraulic fracturing technology in roof with thick and hard sandstone[J]. Jiangxi Coal Science & Technology(2): 116-118,doi: 10.3969/j.issn.1006-2572.2021.02.041. (in Chinese with English abstract)
[12]	LI B, ZHANG W, WEN R, 2022. Study on the hydraulic fracturing in-situ stress measurement in super-long highway tunnels in southern Shaanxi: engineering geological significance[J]. Journal of Geomechanics, 28(2): 191-202,doi: 10.12090/j.issn.1006-6616.2021053. (in Chinese with English abstract)
[13]	LI J W, HE Y, 2021. Analysis and research on in-situ stress measurement based on hydraulic fracturing method[J]. Shanxi Architecture, 47(7): 1-5. (in Chinese with English abstract)
[14]	LI P, MIAO S J, 2017. Analysis and application of in-situ stress in metal mining area of Chinese mainland[J]. Chinese Journal of Engineering, 39(3): 323-334,doi: 10.13374/j.issn2095-9389.2017.03.002. (in Chinese with English abstract)
[15]	LI P, GUO Q F, LIU H T, et al. , 2017. Characteristics of current in-situ stress field and stress accumulation in Shandong region[J]. Chinese Journal of Rock Mechanics and Engineering, 36(9): 2220-2231. (in Chinese with English abstract)
[16]	LI S Q, MA M H, ZHANG X, 2017. In-situ stress distribution regularity of Sanshandao gold mine[J]. Modern Mining, 33(1): 202-205,doi: 10.3969/j.issn.1674-6082.2017.01.056. (in Chinese with English abstract)
[17]	MENG Q, GAO K, CHEN Q Z, et al. , 2021. Seismogenic, coseismic and postseismic deformation and stress evolution of the 2008 Wenchuan earthquake: numerical simulation analysis[J]. Journal of Geomechanics, 27(4): 614-627,doi: 10.12090/j.issn.1006-6616.2021.27.04.051. (in Chinese with English abstract)
[18]	MENG W, TIAN T, SUN D S, et al. , 2022. Research on stress state in deep shale reservoirs based on in-situ stress measurement and rheological model[J]. Journal of Geomechanics, 28(4): 537-549,doi: 10.12090/j.issn.1006-6616.2022041. (in Chinese with English abstract)
[19]	MONTONE P, AMATO A, PONDRELLI S, 1999. Active stress map of Italy[J]. Journal of Geophysical Research, 104(B11): 25595-25610,doi: 10.1029/1999jb900181.
[20]	PENG H, MA X M, JIANG J J, et al. , 2011. Research on stress field and hydraulic fracturing in-situ stress measurement of 1000 m deep hole in Zhaolou coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 30(8): 1638-1645. (in Chinese with English abstract)
[21]	QIN X H, CHEN Q C, ZHAO X G, et al. , 2020. Experimental study on the crucial effect of test system compliance on hydraulic fracturing in-situ stress measurements[J]. Chinese Journal of Rock Mechanics and Engineering, 39(6): 1189-1202,doi: 10.13722/j.cnki.jrme.2019.1204. (in Chinese with English abstract)
[22]	SHANG X G, ZHU S T, JIANG F X, et al. , 2021. Experimental study on the prevention and control of mine earthquake by high pressure water fracturing of huge thick strata in vertical shaft[J]. Journal of China Coal Society, 46(S2): 639-650,doi: 10.13225/j.cnki.jccs.2021.0503. (in Chinese with English abstract)
[23]	SU K Z, 1985. Ground stress measurement methods[M]. Beijing: Seismological Press. (in Chinese)
[24]	WANG C H, GAO G Y, WANG H, et al. , 2020. Integrated determination of principal stress and tensile strength of rock based on the laboratory and field hydraulic fracturing tests[J]. Journal of Geomechanics, 26(2): 167-174,doi: 10.12090/j.issn.1006-6616.2020.26.02.016. (in Chinese with English abstract)
[25]	WANG L J, PAN L Z, 1991. Earth stress measurements and their application in engineering[M]. Beijing: Seismological Press. (in Chinese)
[26]	WANG S J, 2009. Geological Nature of rock and its deduction for rock mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 28(3): 433-450,doi: 10.3321/j.issn:1000-6915.2009.03.001. (in Chinese with English abstract)
[27]	WU M L, MA Y, LIAO C T, et al. , 2008. Study on recent state of stress in depth 1 000 m of Jinchuan mine[J]. Chinese Journal of Rock Mechanics and Engineering, 27(S2): 3785-3790,doi: 10.3321/j.issn:1000-6915.2008.z2.071. (in Chinese with English abstract)
[28]	YIN J M, ZHOU C H, LI Y A, et al. , 2014. Correlation between tunnel stress and regional stress field in North Xinjiang[J]. Journal of Yangtze River Scientific Research Institute, 31(11): 42-46,doi: 10.3969/j.issn.1001-5485.2014.11.009. (in Chinese with English abstract)
[29]	ZHANG C S, WU M L, ZHANG C Y, et al. , 2016. Measurement of present-day stress and analysis of stress state in the Changbaishan Mountains of Jilin province[J]. Chinese Journal of Geophysics, 59(3): 922-930,doi: 10.6038/cjg20160314. (in Chinese with English abstract)
[30]	ZHANG H, SHI G, WU H, et al. , 2020. In-situ stress measurement in the shallow basement of the Shanghai area and its structural geological significance[J]. Journal of Geomechanics, 26(4): 583-594,doi: 10.12090/j.issn.1006-6616.2020.26.04.051. (in Chinese with English abstract)
[31]	ZHANG Y Z, JI H G, ZHANG T Z, et al. , 2019-03-26. A hydraulic fracturing ground stress test device protector: CN, 201821495580.6[P]. (in Chinese)
[32]	ZHAO D A, CHEN Z M, CAI X L, et al. , 2007. Analysis of distribution rule of geostress in China[J]. Chinese Journal of Rock Mechanics and Engineering, 26(6): 1265-1271,doi: 10.3321/j.issn:1000-6915.2007.06.024. (in Chinese with English abstract)
[33]	ZHU H C, TAO Z Y, 1994. State of in-situ stress in different rocks[J]. Acta Seismologica Sinica, 16(1): 49-63. (in Chinese)
[34]	蔡美峰, 1993. 地应力测量原理和方法的评述[J]. 岩石力学与工程学报, 12(3): 275-283.
[35]	蔡美峰, 乔兰, 于波, 等, 1999. 金川二矿区深部地应力测量及其分布规律研究[J]. 岩石力学与工程学报, 18(4): 414-418,doi: 10.3321/j.issn:1000-6915.1999.04.011.
[36]	蔡美峰, 2001. 金属矿山采矿设计优化与地压控制: 理论与实践[M]. 北京: 科学出版社: 1-310.
[37]	蔡美峰, 陈长臻, 彭华, 等, 2006. 万福煤矿深部水压致裂地应力测量[J]. 岩石力学与工程学报, 25(5): 1069-1074,doi: 10.3321/j.issn:1000-6915.2006.05.033.
[38]	陈群策, 安美建, 李方全, 1998. 水压致裂法三维地应力测量的理论探讨[J]. 地质力学学报, 4(1): 37-44.
[39]	盖海龙, 姚生海, 杨丽萍, 等, 2021. 青海玛多“5·22”M_S7.4级地震的同震地表破裂特征、成因及意义[J]. 地质力学学报, 27(6): 899-912,doi: 10.12090/j.issn.1006-6616.2021.27.06.073.
[40]	何满潮, 2004. 深部开采工程岩石力学现状及其展望[C]//第八次全国岩石力学与工程学术大会论文集. 成都: 科学出版社: 99-105.
[41]	侯奎奎, 吴钦正, 张凤鹏, 等, 2022. 不同地应力测试方法在三山岛金矿2 005 m竖井建井区域的应用及其地应力分布规律研究[J]. 岩土力学, 43(4): 1093-1102,doi: 10.16285/j.rsm.2021.1172.
[42]	贾晨, 2021. 厚硬砂岩顶板水压致裂技术的应用[J]. 江西煤炭科技(2): 116-118,doi: 10.3969/j.issn.1006-2572.2021.02.041.
[43]	李彬, 张文, 文冉, 2022. 陕南特长公路隧道水压致裂法地应力测量结果及工程地质意义分析[J]. 地质力学学报, 28(2): 191-202,doi: 10.12090/j.issn.1006-6616.2021053.
[44]	李剑伟, 何勇, 2021. 基于水压致裂法的原地应力测试分析与研究[J]. 山西建筑, 47(7): 1-5. doi: 10.13719/j.cnki.1009-6825.2021.07.001
[45]	李鹏, 苗胜军, 2017. 中国大陆金属矿区实测地应力分析及应用[J]. 工程科学学报, 39(3): 323-334,doi: 10.13374/j.issn2095-9389.2017.03.002.
[46]	李鹏, 郭奇峰, 刘洪涛, 等, 2017. 山东地区现今地应力场特征与应力积累水平分析[J]. 岩石力学与工程学报, 36(9): 2220-2231.
[47]	李书强, 马明辉, 张旭, 2017. 三山岛金矿矿区地应力分布特征[J]. 现代矿业, 33(1): 202-205,doi: 10.3969/j.issn.1674-6082.2017.01.056.
[48]	孟秋, 高宽, 陈启志, 等, 2021. 2008年汶川大地震孕震、同震及震后变形和应力演化全过程的数值模拟[J]. 地质力学学报, 27(4): 614-627,doi: 10.12090/j.issn.1006-6616.2021.27.04.051.
[49]	孟文, 田涛, 孙东生, 等, 2022. 基于原位地应力测试及流变模型的深部泥页岩储层地应力状态研究[J]. 地质力学学报, 28(4): 537-549,doi: 10.12090/j.issn.1006-6616.2022041.
[50]	彭华, 马秀敏, 姜景捷, 等, 2011. 赵楼煤矿1000m深孔水压致裂地应力测量及其应力场研究[J]. 岩石力学与工程学报, 30(8): 1638-1645.
[51]	秦向辉, 陈群策, 赵星光, 等. 2020. 水压致裂地应力测量中系统柔度影响试验研究[J]. 岩石力学与工程学报, 39(6): 1189-1202,doi: 10.13722/j.cnki.jrme.2019.1204.
[52]	尚晓光, 朱斯陶, 姜福兴, 等, 2021. 地面直井水压致裂防控巨厚硬岩运动型矿震试验研究[J]. 煤炭学报, 46(S2): 639-650,doi: 10.13225/j.cnki.jccs.2021.0503.
[53]	苏恺之, 1985. 地应力测量方法[M]. 北京: 地震出版社.
[54]	王成虎, 高桂云, 王洪, 等, 2020. 利用室内和现场水压致裂试验联合确定地应力与岩石抗拉强度[J]. 地质力学学报, 26(2): 167-174,doi: 10.12090/j.issn.1006-6616.2020.26.02.016.
[55]	王连捷, 潘立宙, 1991. 地应力测量及其在工程中的应用[M]. 北京: 地震出版社.
[56]	王思敬, 2009. 论岩石的地质本质性及其岩石力学演绎[J]. 岩石力学与工程学报, 28(3): 433-450,doi: 10.3321/j.issn:1000-6915.2009.03.001.
[57]	吴满路, 马宇, 廖椿庭, 等, 2008. 金川二矿深部1000m中段地应力测量及应力状态研究[J]. 岩石力学与工程学报, 27(S2): 3785-3790,doi: 10.3321/j.issn:1000-6915.2008.z2.071.
[58]	尹健民, 周春华, 李云安, 等, 2014. 北疆深埋隧洞地应力与区域应力场相关性研究[J]. 长江科学院院报, 31(11): 42-46,doi: 10.3969/j.issn.1001-5485.2014.11.009.
[59]	张春山, 吴满路, 张重远, 等, 2016. 长白山地区现今地应力测量结果与应力状态分析[J]. 地球物理学报, 59(3): 922-930,doi: 10.6038/cjg20160314.
[60]	张浩, 施刚, 巫虹, 等, 2020. 上海地区浅部地应力测量及其构造地质意义分析[J]. 地质力学学报, 26(4): 583-594,doi: 10.12090/j.issn.1006-6616.2020.26.04.051
[61]	张月征, 纪洪广, 张同钊, 等, 2019-03-26. 一种水压致裂地应力测试装置保护器: 中国, 201821495580.6[P].
[62]	赵德安, 陈志敏, 蔡小林, 等, 2007. 中国地应力场分布规律统计分析[J]. 岩石力学与工程学报, 26(6): 1265-1271,doi: 10.3321/j.issn:1000-6915.2007.06.024.
[63]	朱焕春, 陶振宇, 1994. 不同岩石中地应力分布[J]. 地震学报, 16(1): 49-63.