A method for determining characteristic pressure parameters during hydraulic fracturing based on linearized fitting
-
摘要: 为了提高水压致裂试验中瞬时闭合压力（ps）与重张压力（pr）等关键参数的识别精度，解决传统方法（如单切线法、平移pb法以及马斯卡特法等）在处理非线性压力–时间曲线中易受噪声干扰、判定主观性强、识别精度不足的问题，提出了一种基于线性化拟合的参数识别方法，通过多项式平滑与分段线性回归将非线性压力–时间曲线转化为若干局部线性段，利用相邻段之间的斜率突变点自动识别ps与pr。该方法分别在室内真三轴水压致裂试验（花岗岩试样）与天津蓟州抽水蓄能电站野外实测（深度范围为75～277 m）中进行了验证。结果表明，线性化拟合方法在ps与pr识别方面具有较高的准确性与稳定性，相较于单切线法、平移pb法和马斯卡特法，平均偏差明显降低，且在存在数据扰动、非线性响应较强的条件下仍表现出良好的鲁棒性。该方法有效提升了参数识别的客观性、一致性和抗干扰能力，适用于硬脆性岩体地应力测量，为水压致裂试验的数据智能识别与解释提供了实用工具，具有良好的工程实用价值和推广前景。Abstract:
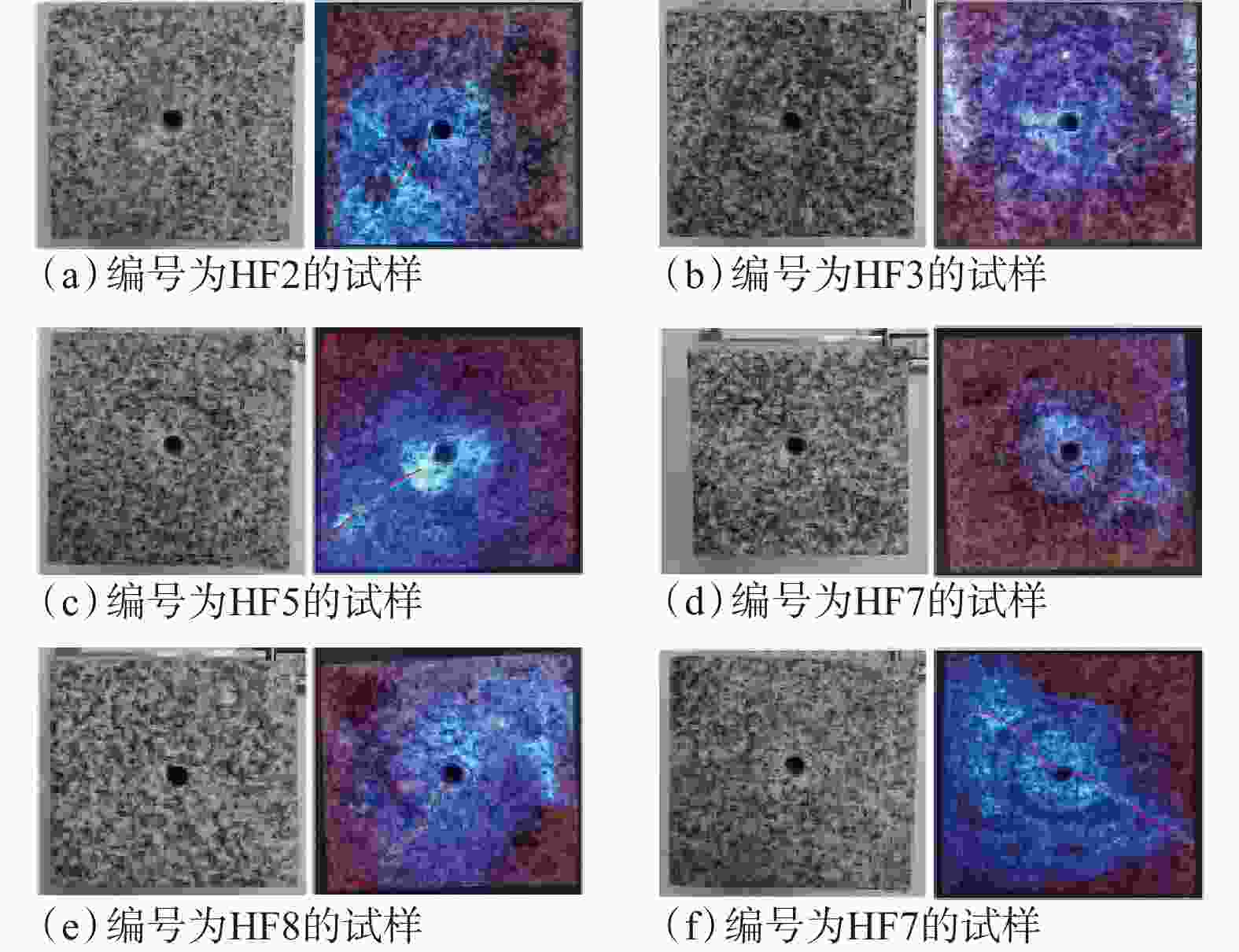
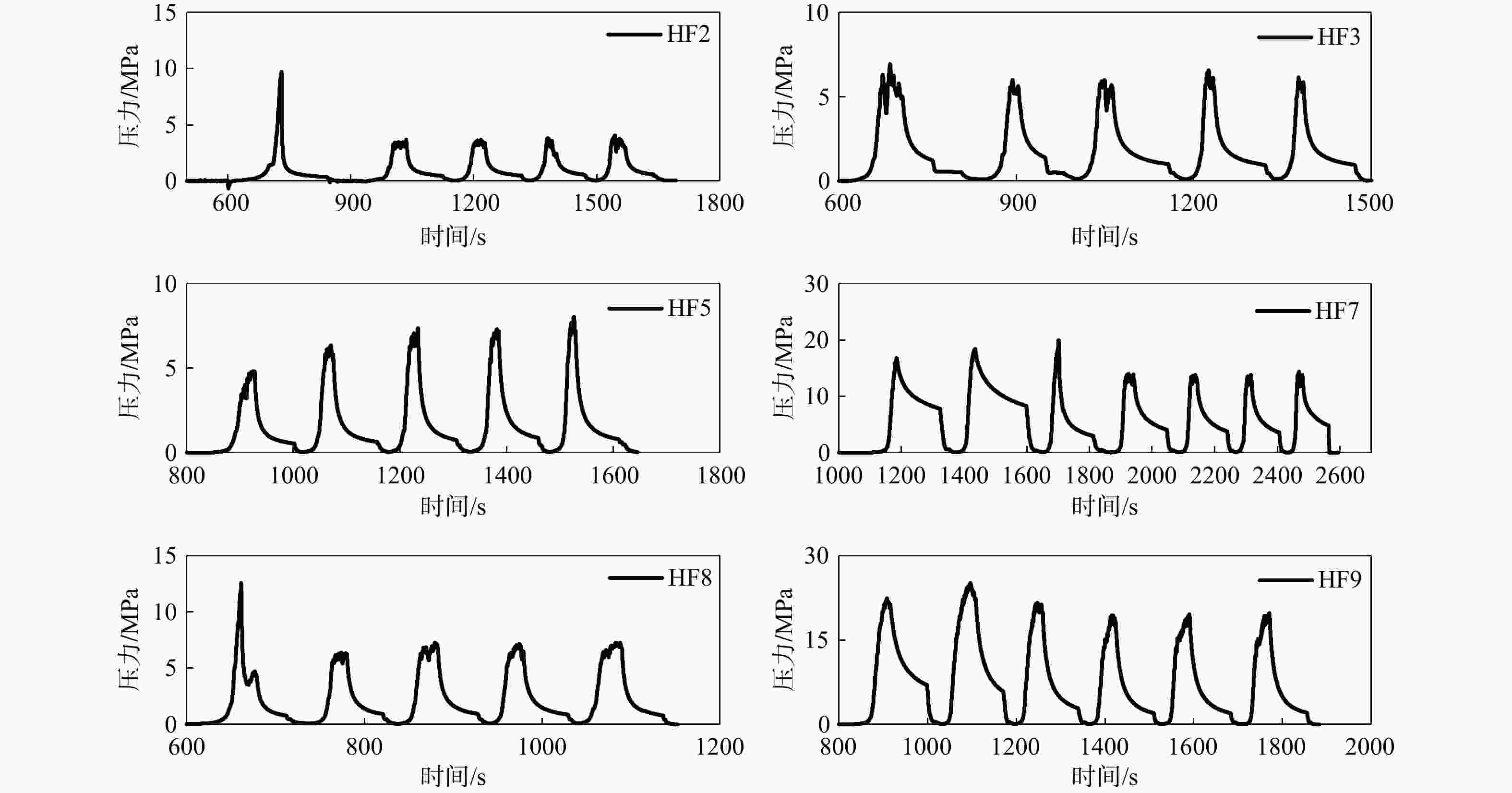
Objective Hydraulic fracturing is a fundamental technique for in-situ stress measurement, yet conventional methods of interpreting the instantaneous shut-in pressure (ps) and reopening pressure (pr) are often sensitive to noise, strongly subjective, and inadequate for facing nonlinear pressure–time responses. To address the lack of objective, robust, and high-accuracy identification methods, this study proposes a linearized curve-fitting approach capable of automatically determining key characteristic pressures from complex fracturing curves. Methods The method transforms a nonlinear pressure–time curve into multiple locally linear segments through polynomial smoothing, adaptive sliding-window regression, and statistical slope-change detection. Significant slope mutations are used to automatically identify ps during the shut-in decay stage and pr during the re-pressurization stage. The method is validated using true-triaxial hydraulic fracturing laboratory tests on granite and field tests at the Jizhou pumped-storage power station (75–277 m depth). Results Across six granite specimens (HF2–HF9), the proposed method consistently produced pr values between those obtained by the single-tangent and shifted-pb methods, avoiding the low–high systematic bias of the two techniques. For ps, the method yielded similar or more conservative results than traditional methods, with most absolute deviations <0.40 MPa. The method demonstrated strong consistency across varying stress states and significantly reduced subjective scatter. The principal stresses calculated from ps and pr showed physically reasonable trends. The σ1 errors were <30% in most cases and the behavior was stable without random jumps, indicating improved objectivity of the automated identification. In the four tested depth intervals of the LFZK02 borehole, pr and ps determined by traditional methods exhibited large spreads (e.g., pr deviations >1.5 MPa and ps deviations up to 0.74 MPa). In contrast, the linearized method consistently produced values close to the multi-method averages and with much smaller dispersion. For ps, deviations relative to Muskat and derivative methods were typically <0.20 MPa. Using the automatically identified ps and pr, the derived principal stresses showed a clear horizontally compressive regime (SH=6.55–9.85 MPa; Sh=3.54–6.21 MPa), matching regional stress data and confirming the reliability of the method in actual field conditions. Conclusion The linearized curve-fitting method effectively overcomes the subjectivity, noise sensitivity, and model-dependence of conventional hydraulic-fracturing interpretation approaches. This method provides stable, accurate, and repeatable identification of ps and pr in both laboratory and field environments and maintains good performance under nonlinear responses, data disturbance, and multi-cycle loading–unloading conditions. [Significance] This study offers a robust, automated, and universally applicable tool for interpreting hydraulic-fracturing pressure curves, significantly enhancing the reliability of in-situ stress measurements and supporting the development of intelligent, standardized stress-testing systems for underground engineering. -
图 1 水压致裂过程中典型压力–时间曲线及关键参数（pb、ps、pr）示意图
Figure 1. Schematic diagram of a typical pressure–time curve and key parameters (pb, ps, pr) during hydraulic fracturing
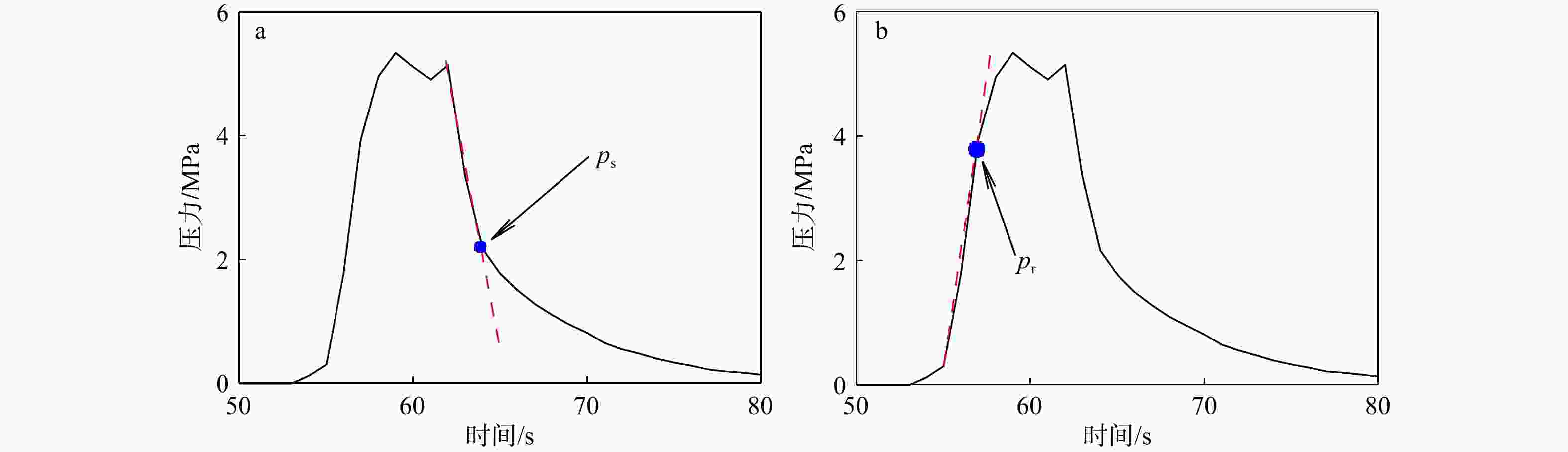
图 2 单切线法识别特征压力的原理示意图
a—降压阶段识别瞬时闭合压力（ps）；b—升压阶段识别重张压力（pr）
Figure 2. Schematic diagrams illustrating the principle of identifying characteristic pressures using the single tangent methode
(a) Identification of the instantaneous shut-in pressure ps during the pressure decline stage; (b) Identification of the reopening pressure pr during the pressurization stage
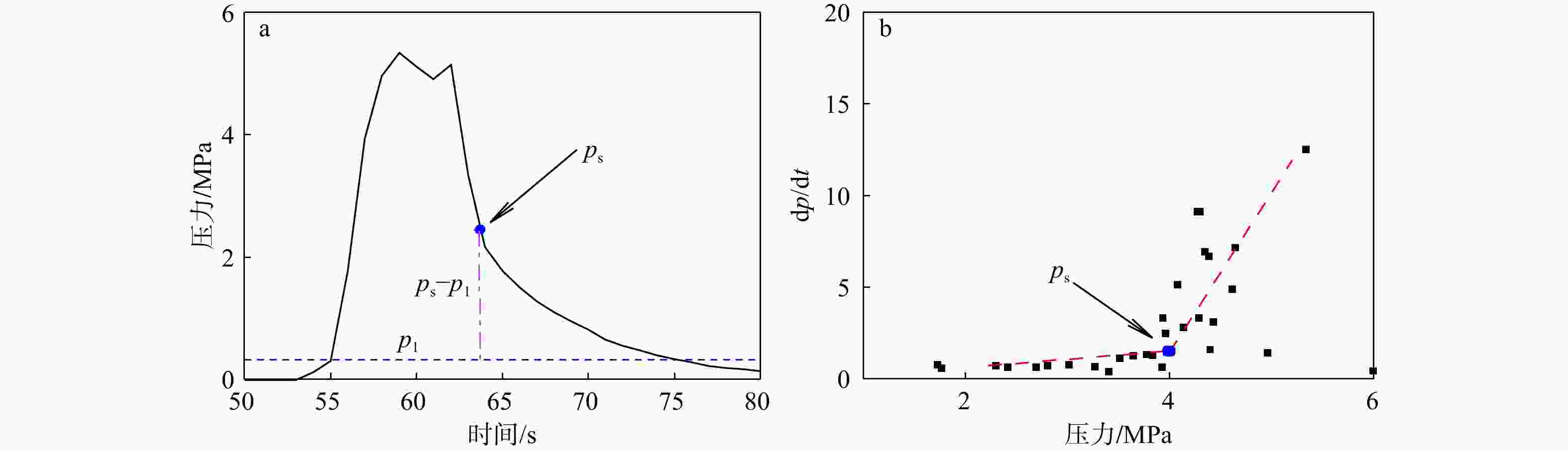
图 3 基于不同方法识别瞬时闭合压力（ps）的原理示意图
p1—压力衰减趋近的稳定值或残余压力a—马斯卡特法的非线性回归拟合；b—导数分析法的dp/dt–压力曲线
Figure 3. Schematic diagrams illustrating the principle of identifying the instantaneous shut-in pressure using different methods (a) Nonlinear regression fitting based on the Muskat method; (b) The dp/dt–p curve based on the derivative analysis method
p1 – the stabilized or residual pressure that the pressure drawdown tends toward
图 4 平移pb法识别重张压力（pr）的原理示意图
Figure 4. Schematic diagram illustrating the principle of identifying the reopening pressure pr using the shifted pb method
图 5 线性化拟合的整体实现流程图
Figure 5. Flowchart of the overall implementation of the linearized curve-fitting method
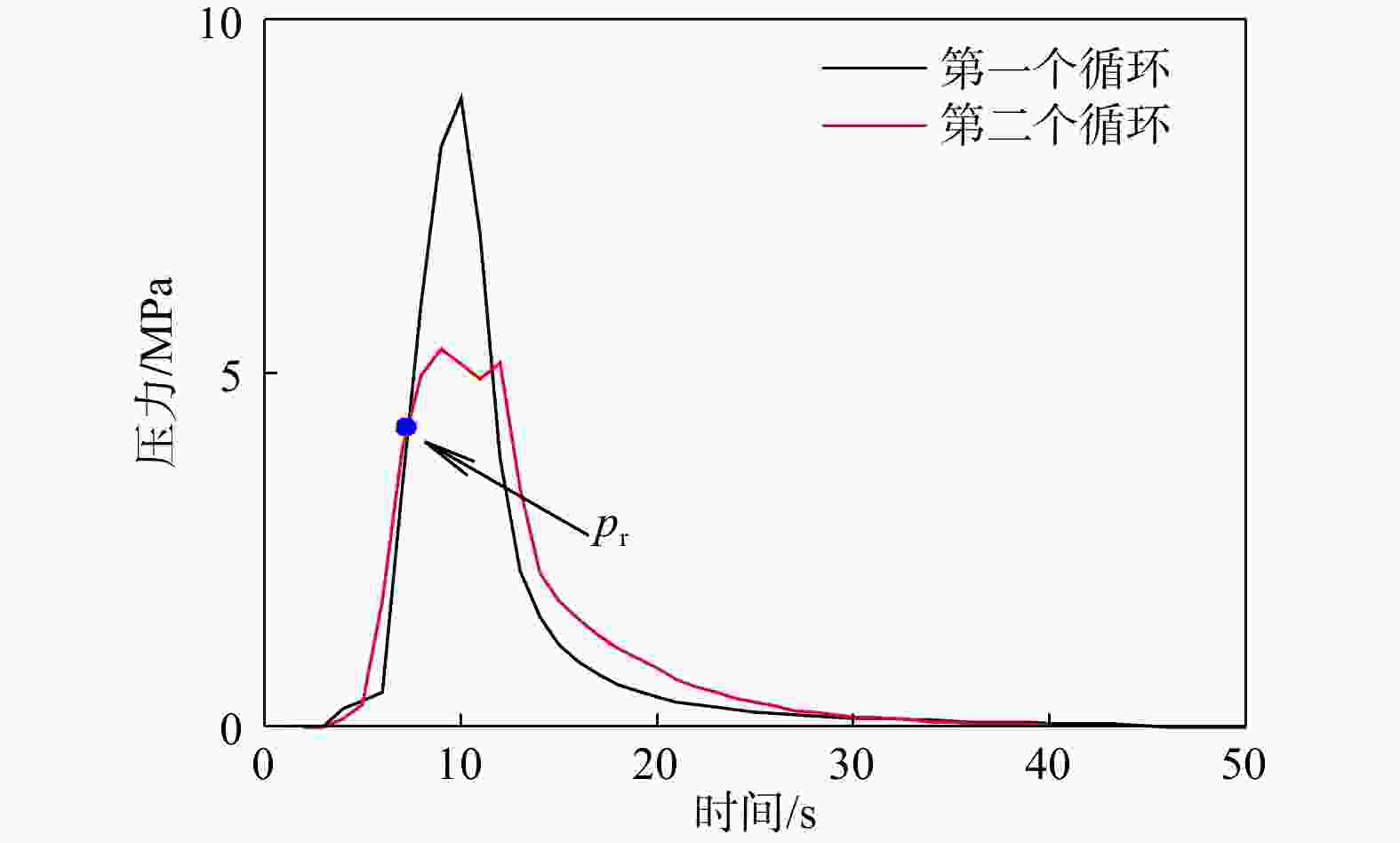
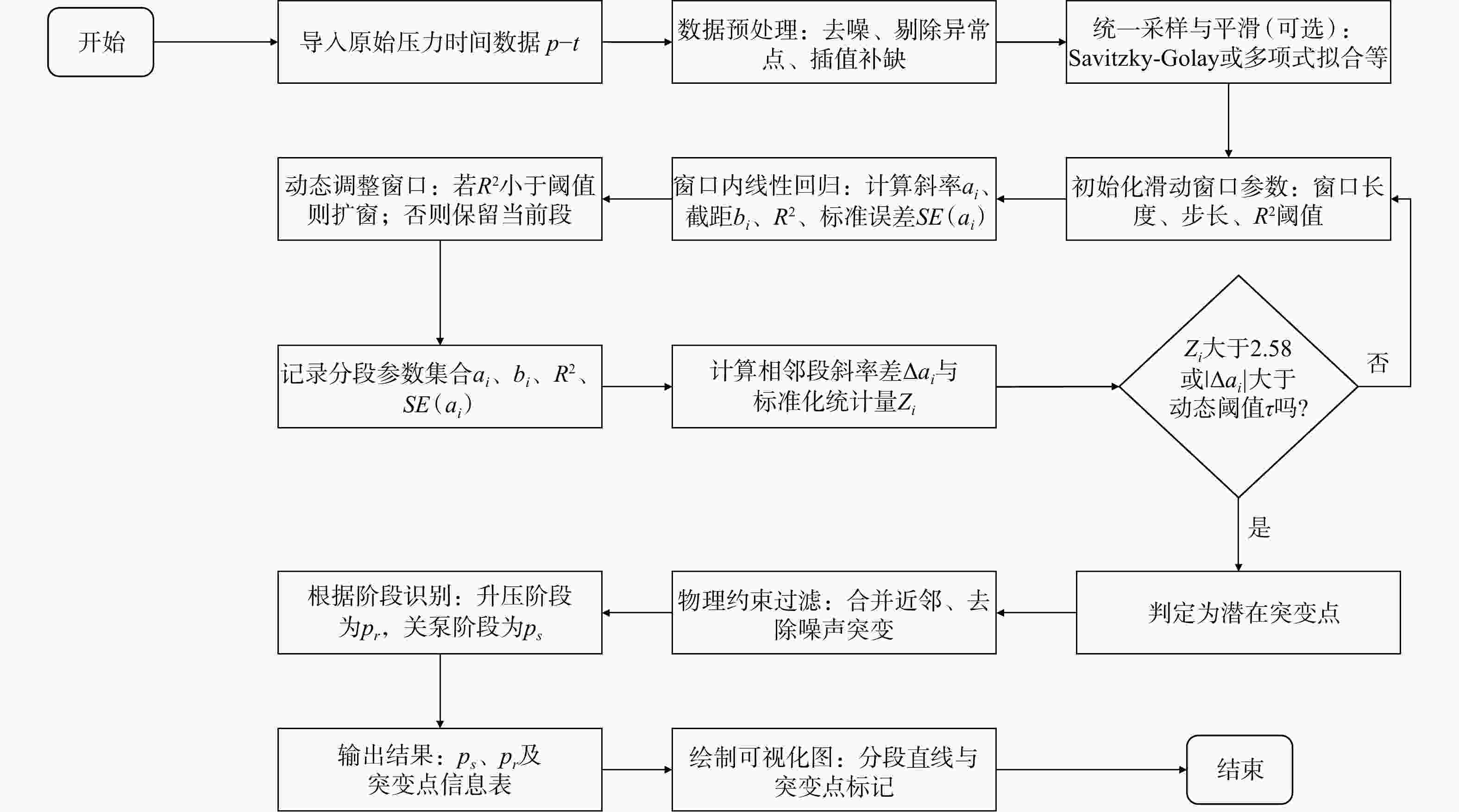
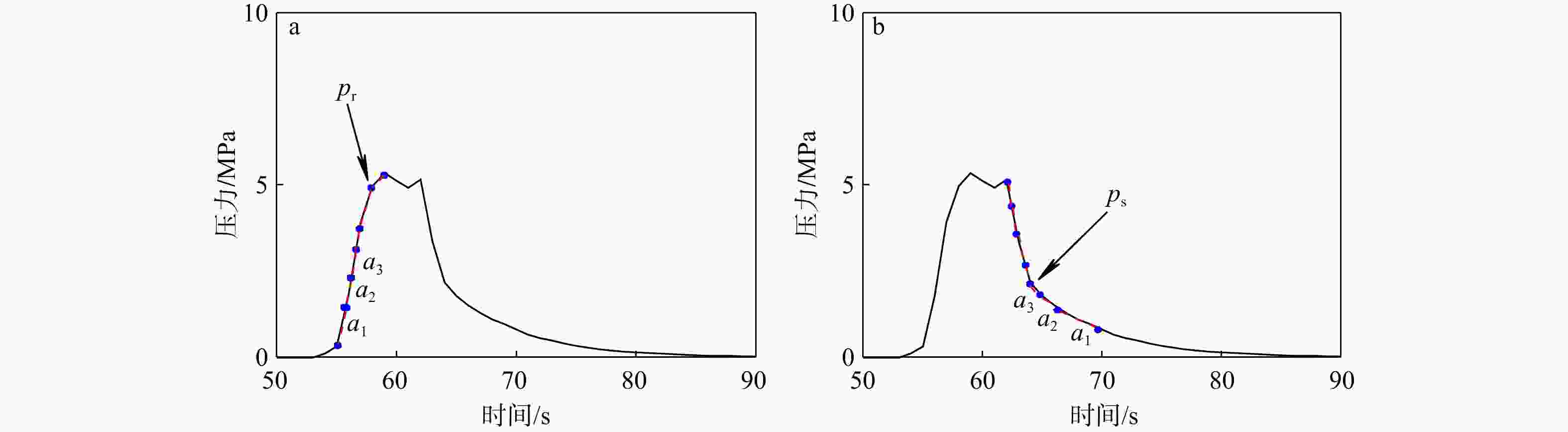
图 6 基于线性化拟合识别特征压力的原理示意图
ai表示第i个数据窗口的斜率，如a1、a2、a3分别表示第1、2、3个数据窗口的斜率a—重张压力pr；b—瞬时闭合压力ps
Figure 6. Schematic diagrams illustrating the principle of identifying characteristic pressures based on the linearized fitting method(a) The reopening pressure pr; (b) The instantaneous shut-in pressure ps
ai denotes the slope of the i-th data window, i.e., a1, a2, and a3 correspond to the slopes of the first, second, and third data windows, respectively.
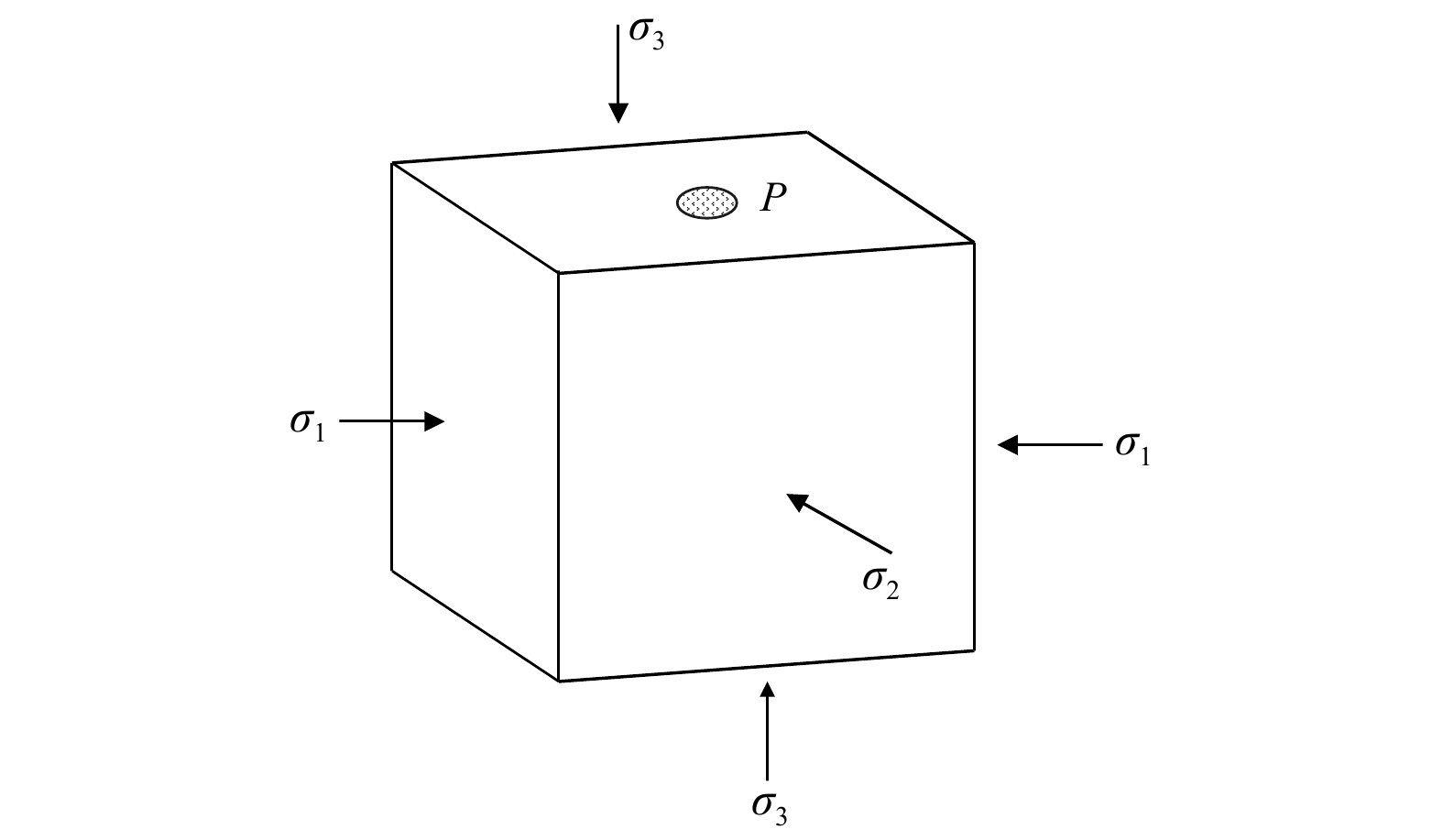
图 7 室内水压致裂试验试样结构示意图
σ1—最大主应力；σ2—最小主应力；σ3—中间主应力；P—注水孔位置，用于施加孔隙压力
Figure 7. Schematic diagram of the specimen structure used in the hydraulic fracturing laboratory test
σ1—maximum principal stress; σ2—minimum principal stress; σ3—intermediate principal stress; P—location of the injection hole for applying pore pressure
图 8 花岗岩试样压裂前后状态对比
Figure 8. Comparison of granite specimens before and after hydraulic fracturing
(a) HF2; (b) HF3; (c) HF5; (d) HF7; (e) HF8; (f) HF9
图 9 水压致裂全过程的压力–时间曲线
Figure 9. Pressure–time curve of the entire hydraulic fracturing process
图 10 线性化拟合法与传统方法平均值之间的绝对偏差对比图
a—重张压力pr；b—瞬时闭合压力ps
Figure 10. Comparison of absolute deviations between the linearized fitting method and the averaged values of the traditional methods
(a) Reopening pressure pr; (b) Instantaneous shut-in pressure ps
图 11 天津蓟州抽水蓄能电站水压致裂测试段岩芯照片
Figure 11. Core samples from hydraulic-fracturing test intervals at the Jizhou Pumped-Storage Power Station, Tianjin (a) 75.2–79.0 m; (b) 84.0–90.0 m; (c) 124.0–131.0 m; (d) 182.7–189.4 m
图 12 天津蓟州龙潭沟LFZK02钻孔现场水压致裂试验压力–时间曲线
Figure 12. Pressure–time curve of the hydraulic fracturing test in the LFZK02 borehole at Longtangou, Jizhou, Tianjin field site
表 1 花岗岩试样室内水压致裂试验加载与注水速率条件
Table 1. Loading conditions and injection rate of granite specimens in hydraulic fracturing laboratory tests
试样编号 $ {\textit{σ}}_{\text{1}} $/MPa $ {\textit{σ}}_{\text{2}} $/MPa $ {\textit{σ}}_{\text{3}} $/MPa 注水速率/(mL/min) HF2 2.40 0.90 1.80 2.20 HF3 3.60 2.00 1.20 2.25 HF5 2.40 1.50 0.90 2.30 HF7 4.80 1.80 2.40 2.00 HF8 3.60 1.20 1.80 2.40 HF9 4.80 3.60 2.40 2.10 注：σ1—最大主应力；σ2—最小主应力；σ3—中间主应力 
下载: 导出CSV
表 2 各方法判读重张压力（pr）与瞬时闭合压力（ps）的结果
Table 2. Reopening pressure (pr) and instantaneous shut-in pressure (ps) determined by various methods
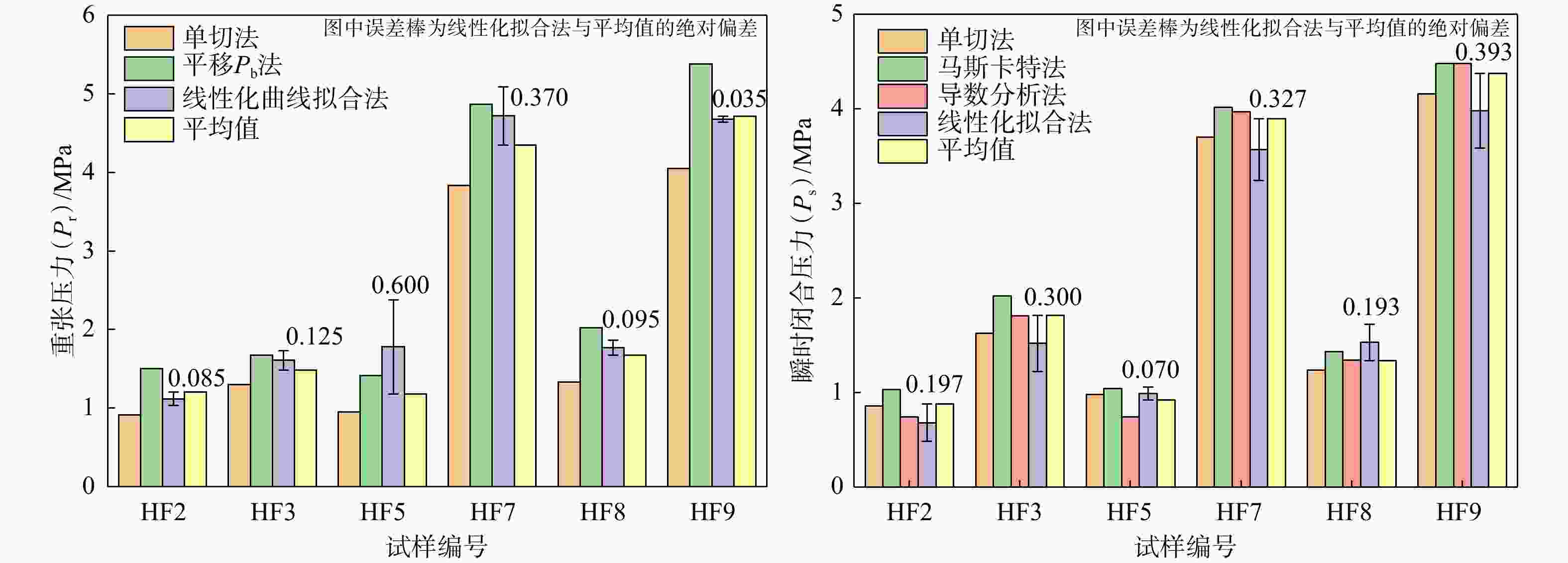
试样编号 pr识别结果/MPa ps识别结果/MPa 单切法 平移pb法 线性化拟合法 单切法 马斯卡特法 导数分析法 线性化拟合法 HF2 0.91 1.50 1.12 0.86 1.03 0.74 0.68 HF3 1.30 1.67 1.61 1.63 2.02 1.81 1.52 HF5 0.95 1.41 1.78 0.98 1.04 0.74 0.99 HF7 3.83 4.87 4.72 3.70 4.02 3.97 3.57 HF8 1.33 2.02 1.77 1.24 1.43 1.34 1.53 HF9 4.05 5.38 4.68 4.16 4.48 4.48 3.98
下载: 导出CSV
表 3 基于线性化拟合法计算的最大主应力（σ1）和最小主应力（σ2）与试验设定值的对比及误差分析
Table 3. Comparison and error analysis for the maximum principal stress σ1 and the minimum principal stress σ2 calculated with the linearized fitting method using the experimental preset values
试样编号 σ1计算结果/MPa σ1试验设定值/MPa σ1相对误差 σ2计算结果/MPa σ2试验设定值/MPa σ2相对误差 HF2 2.33 2.40 3.00% 0.68 0.90 24.44% HF3 2.71 3.60 24.72% 1.52 1.20 26.67% HF5 1.69 2.40 29.58% 0.99 0.90 10.00% HF7 6.48 4.80 35.00% 3.57 1.80 98.33% HF8 3.64 3.60 1.11% 1.53 1.20 27.50% HF9 5.62 4.80 17.08% 3.98 2.40 65.83%
下载: 导出CSV
表 4 现场水压致裂试验中不同方法识别重张压力（pr）与瞬时闭合压力（ps）的结果
Table 4. Reopening pressure (pr) and instantaneous shut-in pressure (ps) identified by different methods in the hydraulic fracturing field test
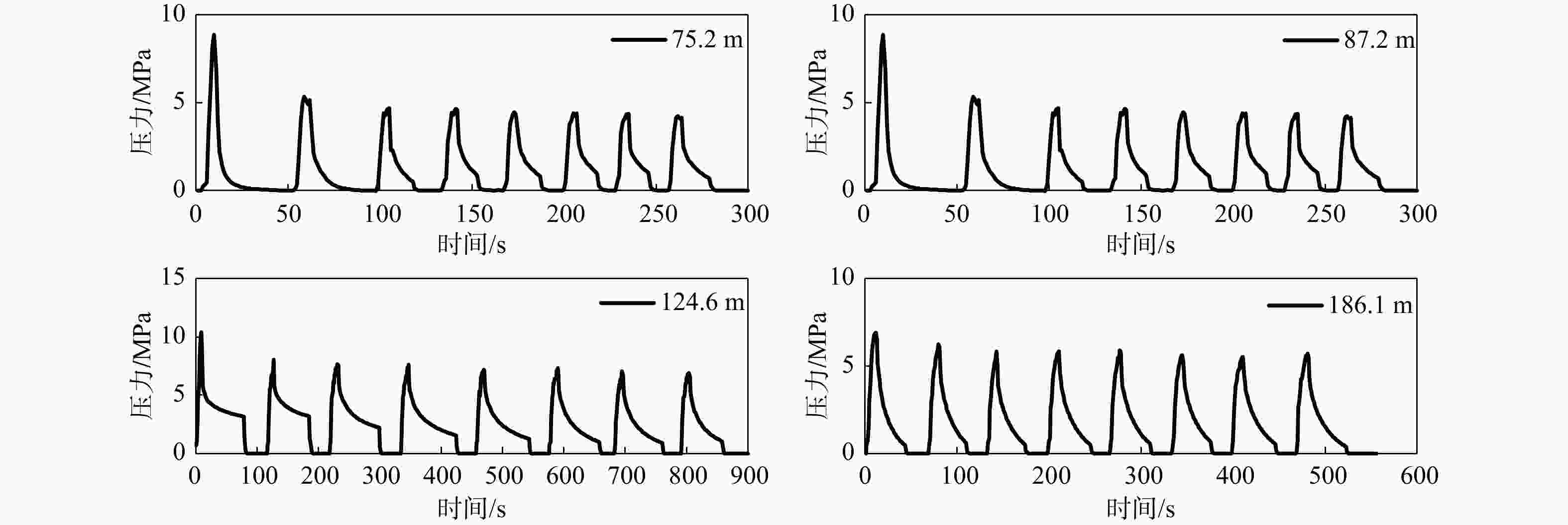
深度/m pr判读数据/MPa ps判读数据/MPa 单切法 平移pb法 平均值 线性化拟合法 单切法 马斯卡特法 导数分析法 平均值 线性化拟合法 75.2 1.48 3.16 2.32 2.61 1.07 1.11 0.96 1.05 1.09 87.2 2.47 4.33 3.40 3.72 2.28 2.39 2.06 2.24 2.12 124.6 3.52 4.92 4.22 4.44 3.82 4.22 3.75 3.93 4.33 186.1 3.80 3.51 3.66 3.29 3.80 3.18 3.20 3.39 3.06
下载: 导出CSV
表 5 线性化拟合法与各判读方法的重张压力（pr）与瞬时闭合压力（ps）偏差比较
Table 5. Comparison of the deviations in reopening pressure (pr) and instantaneous shut-in pressure (ps), as determined by various interpretation methods relative to the linearized fitting method
参数 对比方法 平均偏差/MPa 标准差/MPa 最大偏差/MPa 重张压力（pr） 单切法 0.953 0.282 1.25 平移pb法 0.465 0.148 0.61 瞬时闭合压力（ps） 单切法 0.356 0.284 0.740 马斯卡特法 0.130 0.090 0.270 导数分析法 0.228 0.206 0.580
下载: 导出CSV
表 6 基于线性化拟合法计算的各深度段主应力（ $ {{S}}_{\text{H}} $、$ {{S}}_{\text{h}} $和$ {{S}}_{\text{v}} $）
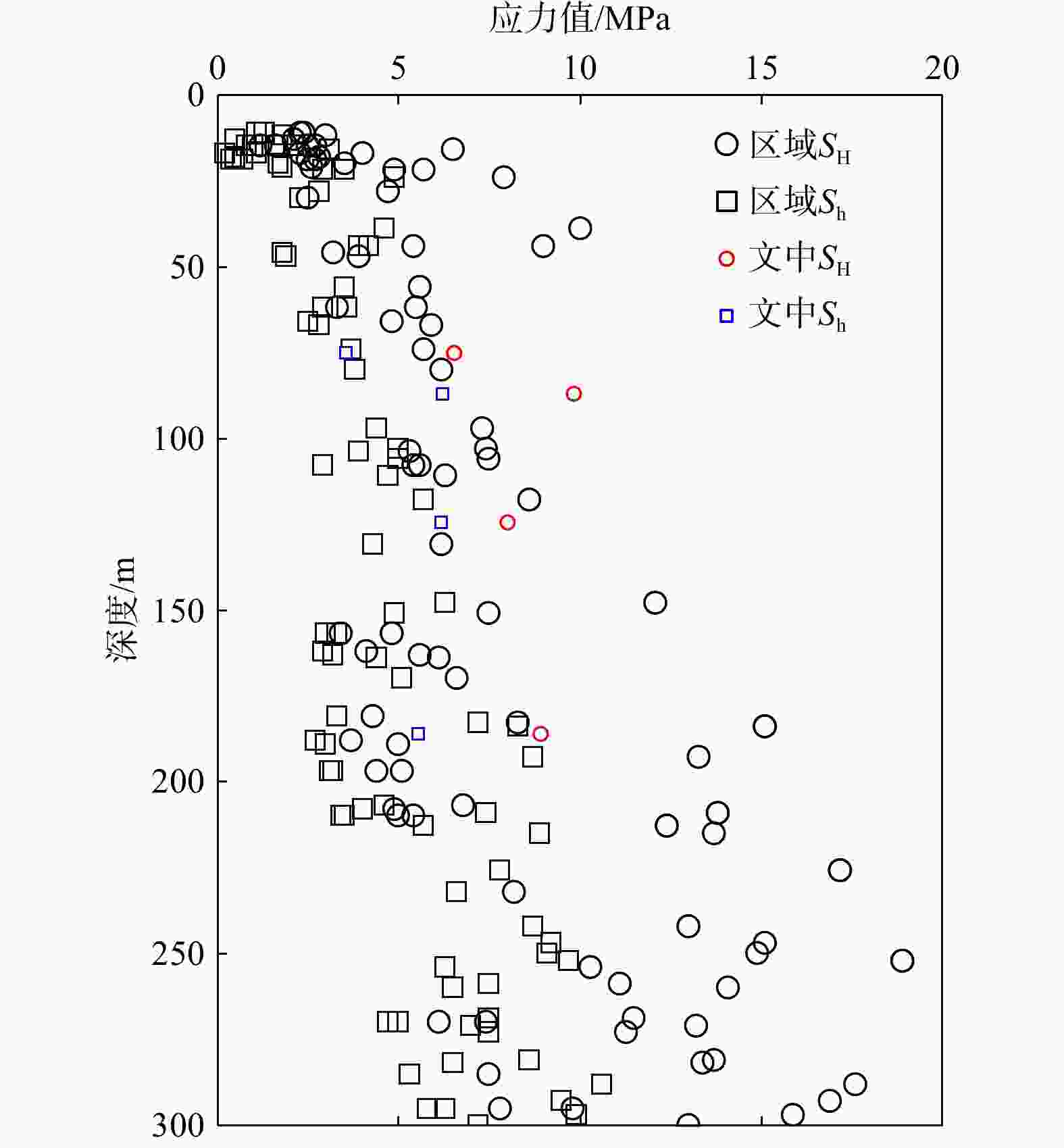
Table 6. Principal stress values SH, Sh, and Sv at various depth intervals calculated based on the linearized curve fitting method
深度/m 最大水平主应力
$ {{S}}_{\text{H}} $/MPa最小水平主应力
$ {{S}}_{\text{h}} $/MPa垂直主应力
$ {{S}}_{\text{v}} $/MPa75.2 6.55 3.54 5.76 87.2 9.85 6.21 6.62 124.6 8.03 6.19 6.53 186.1 8.93 5.56 5.97
下载: 导出CSV
-
[1] AN H Q, SUN D X, ZHANG C T, 2013. Study on several issues in in-situ stress measurement by hydraulic fracturing method[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 35(8): 270-273. (in Chinese with English abstract) [2] CHEN D S, JI H G, YUAN Y Z, et al., 2023. Influence of rock inhomogeneity degree on the crustal stress results measured by hydraulic fracturing method[J]. Journal of Geomechanics, 29(3): 365-374. (in Chinese with English abstract) [3] CHEN Q C, LI F Q, MAO J Z, 2001. Application study of three dimensional geo-stress measurements by use of hydraulic fracturing method[J]. Journal of Geomechanics, 7(1): 69-78. (in Chinese with English abstract) [4] CHEN X Q, 2020. Common errors and its correction of ground stress measurement by hydraulic fracturing method[J]. Railway Engineering, 60(3): 158-161. (in Chinese with English abstract) [5] CHENG Z Y, LIU R, ZHANG J F, et al., 2023. Study on Seepage Mechanism Characteristics of A Single Fracture Based on Fracture Deformation Under Different ConfiningPressures[J]. Geoscience, 37(4): 972-976. (in Chinese with English abstract) [6] FENG C J, CHEN Q C, WU M L, et al., 2012. Analysis of hydraulic fracturing stress measurement data: discussion of methods frequently used to determine instantaneous shut-in pressure[J]. Rock and Soil Mechanics, 33(7): 2149-2159. (in Chinese with English abstract) [7] GABRY M A, ELTALEB I, RAMADAN A, et al., 2024. Hydraulic fracture closure detection techniques: a comprehensive review[J]. Energies, 17(17): 4470. doi: 10.3390/en17174470 [8] GAO G Y, WANG C H, LIU J K, et al., 2024. Determination of the three-dimensional in situ stress tensor in inclined boreholes and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 43(S2): 3700-3709. (in Chinese with English abstract) [9] GUO W D, WANG X J, YANG S X, 2018. Discussion on the development status of hydraulic fracturing method for in-situ stress measurement[J]. Policy Research & Exploration(11): 34-36. (in Chinese with English abstract) [10] HAIMSON B C, CORNET F H, 2003. ISRM suggested methods for rock stress estimation: part 3: hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF)[J]. International Journal of Rock Mechanics and Mining Sciences, 40(7-8): 1011-1020. doi: 10.1016/j.ijrmms.2003.08.002 [11] HE Y R, SONG Z C, ZHANG Y M, et al., 2021. Review on application of machine learning in hydraulic fracturing[J]. Journal of China University of Petroleum (Edition of Natural Science), 45(6): 127-135. (in Chinese with English abstract) [12] LI J W, HE Y, 2021. Analysis and research on in-situ stress measurement based on hydraulic fracturing method[J]. Shanxi Architecture, 47(7): 1-5. (in Chinese with English abstract) [13] LI X Y, LEI X L, LI Q, 2023. Laboratory hydraulic fracturing in layered tight sandstones using acoustic emission monitoring[J]. Geoenergy Science and Engineering, 223: 211510. doi: 10.1016/j.geoen.2023.211510 [14] LIU Y F, 1998. Check and modification for geostress measurement by hydraulic fracturing technique[J]. Chinese Journal of Rock Mechanics and Engineering, 17(3): 297-304. (in Chinese with English abstract) [15] LOU Y, ZHANG G Q, WANG X X, 2017. Study on fracture mechanism of hydraulic fracturing in sandstone by acoustic emission parameters[J]. Procedia Engineering, 191: 291-298. doi: 10.1016/j.proeng.2017.05.184 [16] LEE M Y, HAIMSON B C, 1989. Statistical evaluation of hydraulic fracturing stress measurement parameters[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 26(6): 447-456. [17] MCCLURE M W, JUNG H, CRAMER D D, et al., 2016. The fracture-compliance method for picking closure pressure from diagnostic fracture-injection tests[J]. SPE Journal, 21(4): 1321-1339. doi: 10.2118/179725-PA [18] NADIMI S, FORBES B, MOORE J, et al., 2020. Effect of natural fractures on determining closure pressure[J]. Journal of Petroleum Exploration and Production Technology, 10(2): 711-728. doi: 10.1007/s13202-019-00769-4 [19] NANDE S, 2018. Application of machine learning for closure pressure determination[C]//SPE Annual Technical Conference and Exhibition. Dallas, Texas: SPE. [20] SU H G, LUO L M, 2023. Research status of ground stress test technology[J]. Shaanxi Coal, 42(1): 59-62. (in Chinese with English abstract) [21] WANG C H, WANG X J, BAO L H, et al. , 2014-01-22. System for collecting in-situ stress measurement data by using hydraulic fracturing: CN, CN103527180A[P]. (in Chinese with English abstract) [22] WANG C H, XING B R, JIANG Y H, et al. , 2016. Development and application of interactive software for determination of hydraulic fracturinc stress measurement parameters[C]//Proceedings of the 2016 National Symposium on Engineering Geology. Chengdu: Engineering Geology Professional Committee of the Geological Society of China: 1364-1371. (in Chinese with English abstract) [23] WANG H J, 2003. Study of simulating stress determination technique by hydraulic fracturing method[D]. Qingdao: Shandong University of Science and Technology. (in Chinese with English abstract) [24] WANG Z S, 2019. Study on mechanism and discontinuous deformation analysis of hydraulic fracturing of rock[D]. Ji’nan: Shandong University. (in Chinese with English abstract) [25] WU F P, LI D, FAN X Z, et al., 2020. Analytical interpretation of hydraulic fracturing initiation pressure and breakdown pressure[J]. Journal of Natural Gas Science and Engineering, 76: 103185. doi: 10.1016/j.jngse.2020.103185 [26] XING B R, 2014. Study on three—dimensional geostress determining method with hydraulic fracturing technique in single borehole[D]. Beijing: China University of Geosciences (Beijing). (in Chinese with English abstract) [27] XU B, LIU R M, CHEN Z Y, et al., 2020. Application of pressure transient analysis method in mini-frac test[J]. Journal of Yangtze River Scientific Research Institute, 37(2): 81-86. (in Chinese with English abstract) [28] XIE F R, CHEN Q C, CUI X F, et al., 2007. Fundamental Database of Crustal Stress Environment in the Chinese Mainland[J]. Progress in Geophysics, 01(2007): 131-136. (in Chinese with English abstract) [29] YANG Y H, SUN D S, QIN X H, et al., 2024. Error analysis and discussion of determining the maximum horizontal principal stress by hydraulic fracturing based on the compliance analysis of testing system[J]. Chinese Journal of Rock Mechanics and Engineering, 43(S1): 3385-3396. (in Chinese with English abstract) [30] YE Z, GHASSEMI A, 2025. Laboratory insights on hydraulic fracture closure and stress measurement[J]. Journal of Geophysical Research: Solid Earth, 130(7): e2024JB029854. doi: 10.1029/2024JB029854 [31] ZHANG Y L, TIAN Y, SUN L N, et al., 2025. Research and application of rock fracturing pressure prediction method for deep oil reservoirs[J]. Scientific Reports, 15(1): 10182. doi: 10.1038/s41598-025-94764-x [32] ZHU M D, WANG Z Y, ZHANG Y Z, et al., 2023. In-situ stress measurement and inversion analysis of the deep shaft project area in Sanshan Island based on hydraulic fracturing method[J]. Journal of Geomechanics, 29(3): 430-441. (in Chinese with English abstract) [33] 安贺强, 孙德新, 张春涛, 2013. 水压致裂法地应力测量的几个问题研究[J]. 石油天然气学报(江汉石油学院学报), 35(8): 270-273. [34] 陈东升, 纪洪广, 袁永忠, 等, 2023. 岩石非均质程度对水压致裂地应力测试方法影响的分析与讨论[J]. 地质力学学报, 29(3): 365-374. doi: 10.12090/j.issn.1006-6616.20232906 [35] 陈群策, 李方全, 毛吉震, 2001. 水压致裂法三维地应力测量的实用性研究[J]. 地质力学学报, 7(1): 69-78. doi: 10.3969/j.issn.1006-6616.2001.01.009 [36] 陈兴强, 2020. 水压致裂法地应力测量常见误差与修正[J]. 铁道建筑, 60(3): 158-161. [37] 程智余, 刘瑞, 张金锋, 等, 2023. 围压变化作用下基于水力开度变化的单裂隙渗流特性研究[J]. 现代地质, 37(4): 972-976. [38] 丰成君, 陈群策, 吴满路, 等, 2012. 水压致裂应力测量数据分析: 对瞬时关闭压力Ps的常用判读方法讨论[J]. 岩土力学, 33(7): 2149-2159. doi: 10.3969/j.issn.1000-7598.2012.07.035 [39] 高桂云, 王成虎, 刘冀昆, 等, 2024. 倾斜钻孔三维地应力张量反演方法及其应用研究[J]. 岩石力学与工程学报, 43(S2): 3700-3709. doi: 10.13722/j.cnki.jrme.2023.0900 [40] 郭文雕, 王显军, 杨树新, 2018. 论述原地应力测量水压致裂法发展状况[J]. 决策探索(中)(11): 34-36. [41] 何玉荣, 宋志超, 张燕明, 等, 2021. 机器学习在水力压裂作业中的应用综述[J]. 中国石油大学学报(自然科学版), 45(6): 127-135. doi: 10.3969/j.issn.1673-5005.2021.06.015 [42] 李剑伟, 何勇, 2021. 基于水压致裂法的原地应力测试分析与研究[J]. 山西建筑, 47(7): 1-5. doi: 10.13719/j.cnki.1009-6825.2021.07.001 [43] 刘允芳, 1998. 水压致裂法地应力测量的校核和修正[J]. 岩石力学与工程学报, 17(3): 297-304. [44] 苏宏刚, 罗黎明, 2023. 地应力测试技术研究现状[J]. 陕西煤炭, 42(1): 59-62. doi: 10.3969/j.issn.1671-749X.2023.01.013 [45] 王成虎, 王显军, 包林海, 等, 2014-01-22. 水压致裂法原地应力测量数据采集系统: 中国, CN103527180A[P]. [46] 王成虎, 邢博瑞, 江英豪, 等, 2016. 水压致裂原位应力测量的特征值参数的计算机辅助确定[C]//2016年全国工程地质学术年会论文集. 成都: 中国地质学会工程地质专业委员会: 1364-1371. [47] 汪华君, 2003. 水压致裂法测量地应力模拟方法研究[D]. 青岛: 山东科技大学. [48] 王知深, 2019. 岩石水压致裂的机理研究及非连续变形分析计算[D]. 济南: 山东大学. [49] 邢博瑞, 2014. 单孔三维水压致裂原位地应力测量应用研究[D]. 北京: 中国地质大学(北京). [50] 徐斌, 刘汝明, 陈子扬, 等, 2020. 瞬态压力分析方法在小型压裂地应力测试中的应用[J]. 长江科学院院报, 37(2): 81-86. doi: 10.11988/ckyyb.20181013 [51] 谢富仁, 陈群策, 崔效锋, 等, 2007. 中国大陆地壳应力环境基础数据库[J]. 地球物理学进展, 01(2007): 131-136. doi: 10.3321/j.issn:1000-6915.2004.23.031 [52] 杨跃辉, 孙东生, 秦向辉, 等, 2024. 基于测试系统柔度分析的水压致裂法确定最大水平主应力误差分析与讨论[J]. 岩石力学与工程学报, 43(S1): 3385-3396. doi: 10.13722/j.cnki.jrme.2022.1273 [53] 朱明德, 王照亚, 张月征, 等, 2023. 基于水压致裂法的三山岛深竖井工程区地应力测量与反演分析[J]. 地质力学学报, 29(3): 430-441. doi: 10.12090/j.issn.1006-6616.20232911 -
下载:
计量
- 文章访问数: 110
- HTML全文浏览量: 28
- PDF下载量: 27
- 被引次数: 0
