Review and prospect of structural equation modeling in geoscience data modeling and analysis
-
摘要: 结构方程模型是一种建立、估计和检验因果关系的方法。它可以替代多重回归、路径分析、因子分析、协方差分析等方法,清晰分析单项指标对总体的作用和单项指标间的相互关系,是一种主要应用于验证性模型分析的多元统计建模技术。由于能够通过可观测变量来度量潜变量得分以及分析不同子模型下潜变量之间的协同效应等优点,结构方程模型被广泛应用在心理学、行为学、市场学等领域的数据建模分析研究中,提供了从提出概念—设计模型—获取数据—验证模型的成熟应用路径。地学数据的建模技术一直是地学研究的热点之一,其目的是在海量、多元、高维、多时态的地学数据中,提取出有价值的模型结构以及潜变量,研究不同地学变量以及潜变量之间的交互关系,从而支撑环境治理、灾害防治、资源勘察、生态评价等相关应用和研究。随着地学数据规模变化和建模工具的不断发展,地学数据建模的样本逐渐从抽样建模变为全样本建模,建模方式从有地学模型指导下的建模变为无约束/弱约束建模,建模依据从基于变量因果关系建模变为基于变量相关性的建模,模型复杂度从单模型/单过程建模变为多模型/多过程的综合建模。结构方程模型作为一种综合的建模方法,其可以同时包含因子分析、潜变量估计、路径分析等多种多元分析技术,这种多层次、多分支的建模方法融合了知识驱动建模和数据驱动建模的特点。结构方程模型在地学数据建模中主要面临以下三个方面的挑战,一是从主要面向验证性建模分析的方式向探索性建模分析的方式转变;二是从有完整地学模型约束的建模型方式向弱模型/无模型约束的地学数据建模方式转变;三是从无空间属性的统计变量建模向空间统计变量建模的转变。这对模型本身和数据建模的方法都提出了新的要求。针对以上三个问题,文章在回顾结构方程模型的概念和发展历程的基础上,介绍了三个结构方程模型在地学数据建模中的应用案例,一是利用湖泊沉积物地球化学数据在弱约束条件下提取地球化学金矿内生控矿因子的建模案例;二是利用结构方程模型的综合参数优化方法,通过计算后验概率与观察后验概率的匹配约束来弱化、校正证据权模型中证据独立性问题在计算金矿找矿后验概率中的影响;三是利用结构方程模型来研究墨西哥马格达莱纳流域森林保护策略,通过对不同区域的森林区块进行编号,将空间分布数据转变为传统的无空间属性的统计变量,并分析了不同环境策略对森林保护的影响。Abstract: Structural equation modeling (SEM) is a method of establishing, estimating and testing causality. It can replace multiple regression, path analysis, factor analysis, covariance analysis and other methods to clearly analyze the effect of individual indicators on the overall and the relationship between individual indicators. SEM is a multivariate statistical modeling technology mainly applied to confirmatory factor analysis model. Due to the advantages of measuring latent variable scores through observable variables and analyzing the synergistic effects between latent variables using different sub-models, SEM is widely used in data modeling and analysis in the fields of psychology, behavior, and marketing. It provides a mature application path of proposing the concept-designing the model-obtaining data-verifying the model. Geoscience data modeling technology has always been one of the hotspots in geoscience research, the purpose of which is to extract valuable model structures and latent variables from massive, multi-dimensional, high-dimensional, and multi-temporal geo-data, and to study different geo-variables and interactive relationship between latent variables so as to support related applications and research such as environmental governance, disaster prevention, resource prospecting, and ecological evaluation. With the changes in the scale of geoscience data and the continuous development of modeling tools, the geoscience data modeling have gradually changed from sampling to full-sample, the method from under the guidance of geological models to unconstrained/weak-constrained modeling, the basis from variable causality to variable correlation, and the complexity from single model/single process to comprehensive multi-model/multi-process. SEM is a comprehensive modeling method, which can include multiple analysis techniques such as factor analysis, latent variable estimation, path analysis, etc. This multi-level, multi-branch modeling method combines the characteristics of knowledge-driven modeling and data-driven modeling. SEM generally faces the following three challenges, also three changes, in the modeling of geoscience data: from a method mainly oriented to confirmatory modeling and analysis to an exploratory modeling and analysis method; from a construction with complete geological model constraints to a weak model/unconstrained geological data modeling method; from a modeling of statistical variables without spatial attributes to a modeling of spatial statistical variables. This puts forward new requirements on the model itself and the method of data modeling. In response to the above three issues, this article reviews the concept and development of SEM, and introduces three application cases of SEM in geological data modeling.One is using lake sediment geochemical data to extract mineralization endogenous factors in gold mines which is modeled under weak constraints.The second is using the comprehensive parameter optimization method of SEM to weaken and correct CI problem of weight of evidence in the calculation of the posterior probability of gold prospecting by matching the posterior probability and the observation posterior probability. The third is using SEM to study the forest protection strategy of the Magdalena watershed in Mexico.By numbering the forest blocks in different regions, the spatial distribution of the data is transformed into traditional statistical variables without spatial attributes, and the impact of different environmental strategies on forest protection is analyzed.
-
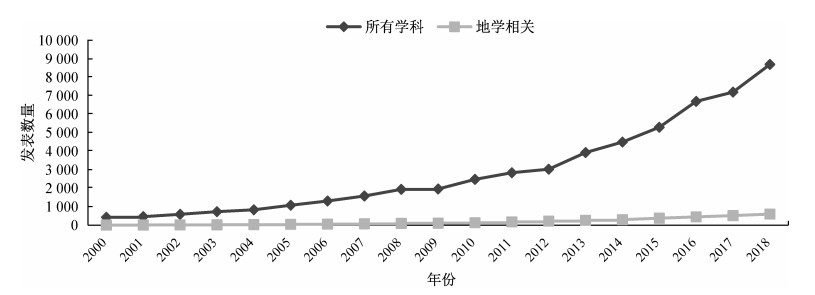
图 1 2000-2018年结构方程模型有关论文在期刊上的发表数量(2000-2009数据来自McArdle and Kadlec, 2013;2009年后数据来自谷歌学术搜索统计)
Figure 1. Number of papers about structural equation models published in journals (2000-2018). (Data of 2000-2009 comes from McArdle and Kadlec, 2013, data after 2009 comes from Google Scholar)
图 3 基于砷元素约束的地球化学内生因子识别模型
输入外源观察变量为Rb、F、Li、Nb、Sn、Zr、Ti、Cu、Pb、Zn、Th、Ag、Sb、Au、W;外源潜变量为LV1-LV3,Rb、Cu、(Au、W)分别为潜变量LV1、LV2、LV3独有识别元素,其他元素为三个潜变量的共有输入元素;LV4为内源潜变量,其外源观察变量为As;外源潜变量LV1-LV3分别代表了成矿物质运输通道、成矿有利元素的赋存地层以及与成矿有关的岩浆作用
Figure 3. Geochemical endogenous factor identification model based on arsenic constraints.The input external observation variables are Rb, F, Li, Nb, Sn, Zr, Ti, Cu, Pb, Zn, Th, Ag, Sb, Au, W. The latent exogenous variables are LV1-LV3. Rb, Cu, (Au, W) are the unique identification elements of the latent variables LV1, LV2 and LV3 respectively, and the other elements are the common input elements of the three latent variables. LV4 is a latent endogenous variable, and its exogenous observed variable is As. The latent variables LV1, LV2 and LV3 respectively represent the ore-forming transport channel, the stratum where the related elements of ore-forming occur, and the magmatism related to ore-forming.
图 4 基于砷元素的三个潜变量结构方程模型的潜变量向量空间
LV1-LV3代表需要求解的外源潜变量,由于LV4仅有As一个内源观察变量,所以直接用As代表用作在路径分析中的约束变量;变量LV1-LV3与As在向量空间中的理想关系为LV1-LV3彼此正交,LV1-LV3与As的夹角尽量小
Figure 4. The latent variable vector space of SEM with three latent variables based on As.LV1-LV3 represent the exogenous latent variables that need to be estimated. Since LV4 has only one endogenous observation variable-As, As is used directly as the constraint variable in the path analysis.The ideal relationships among LV1-LV3 and As in the vector space are: LV1-LV3 are orthogonal to each other, and the angles between LV1-LV3 and As are as small as possible
图 5 基于结构方程模型提取的潜变量与约束变量砷元素的关系(Liu et al., 2015)
Figure 5. The relationship between the latent variable extracted based on SEM and the constrained variable arsenic(Liu et al., 2015)
图 6 基于15种地球化学元素(不含砷)和三个潜变量的预测砷元素得分与观测砷元素回归关系
a-基于15种元素预测砷元素与观测砷元素;b-基于提取的潜变量预测的砷元素与观测砷元素
Figure 6. Regression relationship between observed arsenic and predicted arsenic score based on 15 geochemical elements (without arsenic) and 3 latent variables. (a) Predicted and observed arsenic based on 15 elements. (b) Predicted and observed arsenic based on extracted latent variables
图 7 传统证据权建模过程与基于结构方程模型优化的证据权方法的建模过程(Liu and Cheng, 2019)
Figure 7. The classical weight of evidence modeling process (a) and the modeling process of the weight of evidence method optimized based on SEM (b) (Liu and Cheng, 2019)
图 8 经典证据权和基于结构方程模型约束的证据权模型中预测矿点数-观测矿点数回归模型(Liu and Cheng, 2019)
Figure 8. Regression model of predicted and observed deposits in the classical weight of evidence model (a) and weight of evidence model (b) based on SEM constraints (Liu and Cheng, 2019). The ordinate is the predicted number of deposits, and the abscissa is the observed number of deposits.
图 9 生物多样性状态指标、环境指标、人类压力指标与森林状态关系模型(Santibáñez-Andrade et al., 2015)
Figure 9. Three relationship models based on biodiversity status index, environmental index, human pressure index and forest status(Santibáñez-Andrade et al., 2015)
表 1 多元统计方法的分类(Hair et al., 2016)
Table 1. Classification of multivariate statistical methods (Hair et al., 2016)
探索性分析 确认性分析 第一代 聚类分析
探索性因子分析
多维尺度分析方差分析
逻辑回归分析
多重回归分析第二代 偏最小二乘结构方程模型 确认性因子分析
协方差结构方程模型表 2 文中数学符号说明
Table 2. Definition of notations in the paper
x 外源观察变量(自变量) y 内源观察变量(因变量) ξ 外源潜变量 η 内源潜变量 δ 测量模型(外源观察变量)建模误差 ε 测量模型(内源观察变量)建模误差 ζ 结构模型的建模误差 β, γ 结构模型系数 X 外源观察变量向量(x) Y 内源观察变量向量(y) Ξ 外源潜变量向量(ξ) H 内源潜变量向量(η) Δ, Ε, Z 模型误差向量(δ, ε, ζ) Β, Γ 结构模型系数向量(β, γ) 表 3 森林单元观测指标
Table 3. Indicators of biophysical units
生物多样性状态指标(结构) 生物多样性状态指标(成分) 生物多样性状态指标(功能) 环境指标 人为压力 树层: 树层: -空中生物质 -海拔 -碎片化 -覆盖 -丰富度 -每年垃圾 -坡度 -火灾 -密度 -树种多样性 -ANPP -环境温度 -垃圾 -面积 -重要性指数 -再生 -相对湿度 -放牧 底层: 底层: -生产吨碳/公顷 -光照 -游客 -覆盖 -丰富度 -功能组 -机盖开放因素 -人类活动 -密度 -Alpha多样性 -再生 -全球站点因素 -重要性指数 -土壤pH值 本地,非本地物种和杂草: -导电率 -丰富度 -有机物 -重要性指数 -氮 -磷 -钾 -
AGTERBERG F P, 1989. Systematic approach to dealing with uncertainty of geoscience information retrieval in mineral exploration[C]//Proceedings of the 21st international symposium on applications of computers and operations research in the mineral industry. Las Vegas: AIME: 165-178. AGTERBERG F P, BONHAM-CARTER G F, 1990. Deriving weights of evidence from geoscience contour maps for the prediction of discrete events[C]//Proceedings of the 22nd APCOM symposium. Berlin, Germany: Technical University of Berlin. ALI K, CHENG Q M, CHEN Z J, 2007. Multifractal power spectrum and singularity analysis for modelling stream sediment geochemical distribution patterns to identify anomalies related to gold mineralization in Yunnan Province, South China[J]. Geochemistry: Exploration, Environment, Analysis, 7(4): 293-301. doi: 10.1144/1467-7873/06-116 ANDERSON M J, 2014. Permutational multivariate analysis of variance (PERMANOVA)[M]//Wiley StatsRef: statistics reference online. 1-15. ANDERSON T W, RUBIN H, 1949. Estimation of the parameters of a single equation in a complete system of stochastic equations[J]. Annals of Mathematical Statistics, 20(1): 46-63. doi: 10.1214/aoms/1177730090 ANDERSON T W, RUBIN H, 1950. The asymptotic properties of estimates of the parameters of a single equation in a complete system of stochastic equations[J]. The Annals of Mathematical Statistics, 21(4): 570-582. doi: 10.1214/aoms/1177729752 ATEKWANA E A, SLATER L D, 2009. Biogeophysics: A new frontier in Earth science research[J]. Reviews of Geophysics, 47(4): RG4004. BANDEEN-ROCHE K, MIGLIORETTI D L, ZEGER S L, et al., 1997. Latent variable regression for multiple discrete outcomes[J]. Journal of the American Statistical Association, 92(440): 1375-1386. doi: 10.1080/01621459.1997.10473658 BARILLARI M R, BASTIANI L, LECHIEN J R, et al., 2021. A structural equation model to examine the clinical features of mild-to-moderate COVID-19: A multicenter Italian study[J]. Journal of Medical Virology, 93(2): 983-994. doi: 10.1002/jmv.26354 BASMANN R L, 1957. A generalized classical method of linear estimation of coefficients in a structural equation[J]. Econometrica, 25(1): 77-83. doi: 10.2307/1907743 BOLLEN K, LENNOX R, 1991. Conventional wisdom on measurement: A structural equation perspective[J]. Psychological Bulletin, 110(2): 305-314. doi: 10.1037/0033-2909.110.2.305 BOLLEN K A, PEARL J, 2013. Eight myths about causality and structural equation models[M]//MORGAN S. Handbook of causal analysis for social research. Dordrecht: Springer: 301-328. BONHAM-CARTER G F, AGTERBERG F P, WRIGHT D F, 1988. Integration of geological datasets for gold exploration in Nova Scotia[J]. Photogrammetric Engineering and Remote Sensing, 54(11): 1585-1592. BONHAM-CARTER G F, AGTERBERG F P, WRIGHT D F, 1989. Weights of evidence modeling: a new approach to mapping mineral potential[M]//AGTERBERG F P, BONHAM-CARTER G F. Statistical applications in the earth sciences. Ottawa: Canadian Government Publishing Centre: 171-183. BONHAM-CARTER G F, 2014. Geographic information systems for geoscientists. Modelling with GIS[M]. Tarrytown, N. Y. : Elsevier Science Ltd. BROWNE M W, ARMINGER G, 1995. Specification and estimation of mean-and covariance-structure models[M]//ARMINGER G, CLOGG C C, SOBEL M E. Handbook of statistical modeling for the social and behavioral sciences. Boston, MA: Springer: 185-249. ÇAKIT E, OLAK A J, KARWOWSKI W, et al., 2020. Assessing safety at work using an adaptive neuro-fuzzy inference system (ANFIS) approach aided by partial least squares structural equation modeling (PLS-SEM)[J]. International Journal of Industrial Ergonomics, 76: 102-925. CHEN G X, TIAN Y P, ZHANG X L, et al., 2019. Rapid construction and uncertainty analysis of 3D geological models based on exploration sections[J]. Geological Science and Technology Information, 38(2): 275-280. (in Chinese with English abstract) CHENG Q, 1994. Multifractal modelling and spatial analysis with GIS: Gold potential estimation in the Mitchell-Sulphurets area, northwestern British Columbia[D]. Ottawa: University of Ottawa (Canada). CHENG Q M, 1999. Spatial and scaling modelling for geochemical anomaly separation[J]. Journal of Geochemical Exploration, 65(3): 175-194. doi: 10.1016/S0375-6742(99)00028-X CHENG Q M, 2007a. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China[J]. Ore Geology Reviews, 32(1-2): 314-324. doi: 10.1016/j.oregeorev.2006.10.002 CHENG Q M, 2007b. Multifractal imaging filtering and decomposition methods in space, Fourier frequency, and eigen domains[J]. Nonlinear Processes in Geophysics, 14(3): 293-303. doi: 10.5194/npg-14-293-2007 CHENG Q M, 2008. Non-linear theory and power-law models for information integration and mineral resources quantitative assessments[J]. Mathematical Geosciences, 40(5): 503-532. doi: 10.1007/s11004-008-9172-6 CHENG Q M, BONHAM-CARTER G, WANG W L, et al., 2011. A spatially weighted principal component analysis for multi-element geochemical data for mapping locations of felsic intrusions in the Gejiu mineral district of Yunnan, China[J]. Computers & Geosciences, 37(5): 662-669. CHENG Q M, 2012a. Ideas and methods for mineral resources integrated prediction in covered areas[J]. Earth Science-Journal of China University of Geosciences, 37(6): 1109-1125. (in Chinese with English abstract) CHENG Q M, 2012b. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas[J]. Journal of Geochemical Exploration, 122: 55-70. doi: 10.1016/j.gexplo.2012.07.007 CHENG Q M, 2014. Vertical distribution of elements in regolith over mineral deposits and implications for mapping geochemical weak anomalies in covered areas[J]. Geochemistry: Exploration, Environment, Analysis, 14(3): 277-289. doi: 10.1144/geochem2012-174 CHIN W W, 1998. The partial least squares approach to structural equation modeling[M]//MARCOULIDES M A. Modern methods for business research. Mahwah, NJ: Lawrence Erlbaum Associates: 295-336. CHRIST C F, 1994. The Cowles Commission's contributions to econometrics at Chicago, 1939-1955[J]. Journal of Economic Literature, 32(1): 30-59. DEL CAMPO A G, 2016. GIS in environmental assessment: a review of current issues and future needs[J]. Journal of Environmental Assessment Policy and Management (JEAPM), 14(1): 1-23. FAREBROTHER R W, 1999. A class of statistical estimators related to principal components[J]. Linear Algebra and Its Applications, 289(1-3): 121-126. doi: 10.1016/S0024-3795(97)10006-4 FERRERO R C, KOLAK J J, BILLS D J, et al. 2013. U.S. Geological Survey Energy and Minerals science strategy: A resource lifecycle approach (1383D)[R]. Reston, VA: U.S. Geological Survey. FORNELL C, WERNERFELT B, 1987. Corporate consumer affairs departments: retrospect and prospect, & Quot[M]//MAYNES E S. Research in the consumer interest: the frontier. Ann Arbor, MI: Association for Consumer Research: 337-346. HART J K, MARTINEZ K, 2006. Environmental sensor networks: A revolution in the earth system science?[J]. Earth-Science Reviews, 78(3-4): 177-191. doi: 10.1016/j.earscirev.2006.05.001 HAIR JR J F, HULT G T M, RINGLE C M, et al., 2016. A primer on partial least squares structural equation modeling (PLS-SEM)[M]. 2nd ed. Thousand Oaks, CA: Sage Publications Inc. HAIR JR J F, PAGE M, BRUNSVELD N, 2019. Essentials of business research methods[M]. 4th ed. New York: Routledge. JAAFARI S, SHABANI A A, MOEINADDINI M, et al., 2020. Applying landscape metrics and structural equation modeling to predict the effect of urban green space on air pollution and respiratory mortality in Tehran[J]. Environmental Monitoring and Assessment, 192(7): 412. doi: 10.1007/s10661-020-08377-0 JENSEN J R, 2007. Remote sensing of the environment: An earth resource perspective[M]. 2nd ed. Singapore: Pearson Education India. JÖRESKOG K G, 1970. A general method for analysis of covariance structures[J]. Biometrika, 57(2): 239-251. doi: 10.1093/biomet/57.2.239 KOOPMANS T C, HOOD W C, 1953. The estimation of simultaneous linear economic relationships[M]//HOOD W C, KOOPMANS T C. Cowles commission monograph no. 14: studies in econometric method. New York: J. Wiley and Sons: 112-199. LEE S Y, SHI J Q, 2001. Maximum likelihood estimation of two-level latent variable models with mixed continuous and polytomous data[J]. Biometrics, 57(3): 787-794. doi: 10.1111/j.0006-341X.2001.00787.x LIU G, WU C L, HE Z W, et al., 2020. Data model for geological spatiotemporal big data expression and storage management[J]. Bulletin of Geological Science and Technology, 39(1): 164-174. (in Chinese with English abstract) LIU J T, CHENG Q M, WANG J G, 2015. Identification of geochemical factors in regression to mineralization endogenous variables using structural equation modeling[J]. Journal of Geochemical Exploration, 150: 125-136. doi: 10.1016/j.gexplo.2014.12.021 LIU J T, WU F F, WANG J X, et al., 2017. Design of a geochemical data processing model based on ArcGIS model builder and its application in morocco geochemical mapping project[J]. Geological Science and Technology Information, 36(5): 1-6. (in Chinese with English abstract) LIU J T, CHENG Q M, 2019. A modified weights-of-evidence method for mineral potential prediction based on structural equation modeling[J]. Natural Resources Research, 28(3): 1037-1053. doi: 10.1007/s11053-018-9435-y LOHMÖLLER J B, 2013. Latent variable path modeling with partial least squares[M]. Springer Science & Business Media. MCARDLE J J, KADLEC K M, 2013. Structural equation models[M]. Oxford: The Oxford Handbook of Quantitative Methods, 2: 295-337. MUTHÉN B, 1984. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators[J]. Psychometrika, 49(1): 115-132. doi: 10.1007/BF02294210 OSMAN A R, SOHEL-UZ-ZAMAN A S, ASHRAF M A, et al., 2020. Vindicating service quality of education through Structural Equation Modeling (SEM): international students' perspective[J]. International Journal of Higher Education, 9(3): 158-172. doi: 10.5430/ijhe.v9n3p158 PEARL J, 2009. Causal inference in statistics: An overview[J]. Statistics Surveys, 3: 96-146. PLOHL N, MUSIL B, 2021. Modeling compliance with COVID-19 prevention guidelines: the critical role of trust in science[J]. Psychology, Health & Medicine, 26(1): 1-12. SAMMEL M D, RYAN L M, 1996. Latent variable models with fixed effects[J]. Biometrics, 52(2): 650-663. doi: 10.2307/2532903 SANCHEZ B N, BUDTZ-JØRGENSEN E, RYAN L M, et al., 2005. Structural equation models: a review with applications to environmental epidemiology[J]. Journal of the American Statistical Association, 100(472): 1443-1455. doi: 10.1198/016214505000001005 SANTIBÁÑEZ-ANDRADE G, CASTILLO-ARGVERO S, VEGA-PEÑA E V, et al., 2015. Structural equation modeling as a tool to develop conservation strategies using environmental indicators: The case of the forests of the Magdalena river basin in Mexico City[J]. Ecological Indicators, 54: 124-136. doi: 10.1016/j.ecolind.2015.02.022 SARGAN J D, 1958. The instability of the Leontief dynamic model[J]. Econometrica, 26(3): 381-392. doi: 10.2307/1907618 SUN D, CHEN Q, ZHANG Y, 2020. Analysis on the application prospect of ASR in-situ stress measurement method in underground mine[J]. Journal of Geomechanics, 26(1): 33-38. (in Chinese with English abstract) THEIL H, 1953. Repeated least squares applied to complete equation systems[M]. The Hague: Central Planning Bureau (Mimeo). WANG W L, CHENG Q M, 2008. Mapping mineral potential by combining multi-scale and multi-source geo-information[C]//IGARSS 2008-2008 IEEE international geoscience and remote sensing symposium. Boston, MA, USA: IEEE. WANG Y A, RHEMTULLA M, 2021. Power analysis for parameter estimation in structural equation modeling: A discussion and tutorial[J]. Advances in Methods and Practices in Psychological Science, 4(1). doi: 10.1177/2515245920918253. WOLD H, 1966. Estimation of principal components and related models by iterative least squares[M]//KRISHNAJAH P R. Multivariate analysis. NewYork: Academic Press: 391-420. WRIGHT S, 1918. On the nature of size factors[J]. Genetics, 3(4): 367-374. doi: 10.1093/genetics/3.4.367 WRIGHT S, 1920. The relative importance of heredity and environment in determining the piebald pattern of guinea-pigs[J]. Proceedings of the National Academy of Sciences of the United States of America, 6(6): 320-332. doi: 10.1073/pnas.6.6.320 WRIGHT S, 1921a. Systems of mating. I. The biometric relations between parent and offspring[J]. Genetics, 6(2): 111-123. doi: 10.1093/genetics/6.2.111 WRIGHT S, 1921b. Systems of mating. II. The effects of inbreeding on the genetic composition of a population[J]. Genetics, 6(2): 124-143. doi: 10.1093/genetics/6.2.124 WU C L, LIU G, WANG L Z, et al., 2020. Thinking and methods of intelligent supervision of urban geological environment based on big data[J]. Bulletin of Geological Science and Technology, 39(1): 157-163. (in Chinese with English abstract) XIN L, LIU X X, ZHANG B, 2021. Land surface temperature retrieval and geothermal resources prediction by remote sensing image: A case study in the Shijiazhuang area, Hebei province[J]. Journal of Geomechanics, 27(1): 40-51. (in Chinese with English abstract) IAO H, ZHANG Y, KONG D S, et al., 2020. The effects of social support on sleep quality of medical staff treating patients with coronavirus disease 2019 (COVID-19) in January and February 2020 in China[J]. Medical Science Monitor, 26: e923549-923541. YANG F, WANG H, HUANG B, et al., 2019. Study on the stress sensitivity and seepage characteristics of tight sandstone based on CT scanning[J]. Journal of Geomechanics, 25(4): 475-482. (in Chinese with English abstract) YUAN K H, BENTLER P M, 1997. Mean and covariance structure analysis: Theoretical and practical improvements[J]. Journal of the American Statistical Association, 92(438): 767-774. doi: 10.1080/01621459.1997.10474029 YUAN K H, BENTLER P M, 2000. Three likelihood-based methods for mean and covariance structure analysis with nonnormal missing data[J]. Sociological Methodology, 30(1): 165-200. doi: 10.1111/0081-1750.00078 ZHANG D, LI J C, WU Z H, et al., 2021. Using terrestrial LiDAR to accurately measure the micro-geomorphologic geometry of active fault: A case study of fault scarp on the Maoyaba fault zone[J]. Journal of Geomechanics, 27(1): 63-72. (in Chinese with English abstract) ZHAO F S, HUA S, WU H, et al., 2021. Quantitative prediction of the undiscovered epithermal gold (silver) mineral resources in Sumatra, Indonesia[J]. Bulletin of Geological Science and Technology, 40(1): 119-131. (in Chinese with English abstract) 陈国旭, 田宜平, 张夏林, 等, 2019. 基于勘探剖面的三维地质模型快速构建及不确定性分析[J]. 地质科技情报, 38(2): 275-280. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201902033.htm 成秋明, 2012. 覆盖区矿产综合预测思路与方法[J]. 地球科学(中国地质大学学报), 37(6): 1109-1125. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX201206005.htm 刘刚, 吴冲龙, 何珍文, 等, 2020. 面向地质时空大数据表达与存储管理的数据模型研究[J]. 地质科技通报, 39(1): 164-174. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202001020.htm 刘江涛, 吴发富, 王建雄, 等, 2017. 基于ArcGIS建模器的数据处理模型在摩洛哥地球化学填图中的应用[J]. 地质科技情报, 36(5): 1-6. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201705001.htm 孙东生, 陈群策, 张延庆, 2020. ASR法在井下矿山地应力测试中的应用前景分析[J]. 地质力学学报, 26(1): 33-38. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX202001004.htm 吴冲龙, 刘刚, 王力哲, 等, 2020. 基于大数据的城市地质环境智能监管思路与方法[J]. 地质科技通报, 39(1): 157-163. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202001019.htm 辛磊, 刘新星, 张斌, 2021. 遥感影像地表温度反演与地热资源预测: 以石家庄地区为例[J]. 地质力学学报, 27(1): 40-51. https://www.cnki.com.cn/Article/CJFDTOTAL-QXXX201310008.htm 杨峰, 王昊, 黄波, 等, 2019. 基于CT扫描的致密砂岩渗流特征及应力敏感性研究[J]. 地质力学学报, 25(4): 475-482. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201904003.htm 张迪, 李家存, 吴中海, 等, 2021. 利用地面LiDAR精细化测量活断层微地貌形态: 以毛垭坝断裂禾尼处断层崖为例[J]. 地质力学学报, 27(1): 63-72. 赵风顺, 华杉, 吴昊, 等, 2021. 印度尼西亚苏门答腊岛浅成低温热液型金(银)矿产资源总量预测[J]. 地质科技通报, 40(1): 119-131. -





 下载:
下载: