离心模型试验模拟塑料排水板处理软土地基的方法和应用

王存; 侯瑜京; 刘国宝; 彭仁

离心模型试验模拟塑料排水板处理软土地基的方法和应用

1.
中国水利水电科学研究院岩土工程研究所, 北京 100048
2.
中交水运规划设计院有限公司, 北京 100007
3.
北京航空航天大学土木工程系, 北京 100191

基金项目:

国家重点基础研究发展计划(973计划)项目 2012CB719803

详细信息

作者简介:
王存(1990-), 硕士研究生, 主要从事土工离心模型试验相关研究。E-mail:1261821773@qq.com

中图分类号: P642.1
计量
- 文章访问数: 108
- HTML全文浏览量: 77
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2015-10-26
- 刊出日期: 2016-03-28

THE METHOD AND APPLICATION OF CENTRIFUGAL MODELING TO VERTICAL STRIP DRAINS IN SOFT FOUNDATION

1.
Department of Geotechnical Engineering, China Institute of Water Resources and Hydropower Research, Beijing 100048, China
2.
CCCC Water Transportation Consultants Co., Ltd, Beijing 100007, China
3.
Department of Civil Engineering, Beihang University, Beijing 100191, China

摘要

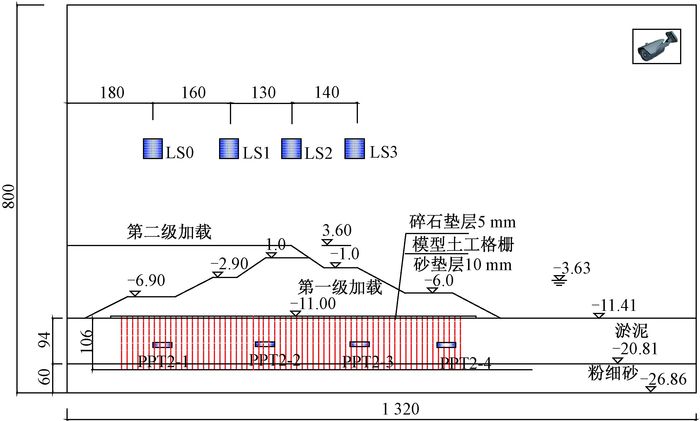
摘要: 采用大型土工离心机对某工程近海软土地基上堤坝施工期及运行期进行了模拟。试验中采用停机加载法模拟分级施工加载过程, 原型中采用塑料排水板固结法处理软土地基, 模型中则根据固结过程相似的原理, 换算成等效圆截面排水体, 在模型制作中采用等效透水滤芯进行模拟。根据激光位移传感器和孔隙水压力传感器数据可以得出相应原型软土地基的沉降特性和孔隙水压力变化情况。根据试验得到的沉降曲线, 采用"经验双曲线法"推算出了地基最终沉降, 然后得出按沉降推算的分层地基平均固结度随时间的变化。对比试验模拟得到的软土地基固结度和理论计算结果, 二者基本接近, 表明塑料排水板模拟方法用于离心模型试验是可行的。
- 塑料排水板 /
- 离心模型试验 /
- 软土地基 /
- 固结度
Abstract: Centrifuge model tests were carried out to simulate the construction and operation of the dike on a soft soil foundation by using the geotechnical centrifuge in IWHR. The vertical strip drains in the foundation were simulated by a kind of model cylinder vertical drains, based on the principle of same consolidation degree in the foundation in average for both type of drains. During the model tests, the construction processes were simulated by loading dike materials layer by layer when the centrifuge stops running. Laser displacement sensors and the pore pressure transducers were installed for model measurement of settlement and pore pressure variation during tests. Based on the measured data, the final settlement of the dike was estimated by using experience hyperbolic method. And the consolidation degree of the foundation over time was also calculated, which indicates the average consolidation of the sludge and the sand under the dike. Comparing the consolidation degree of the soft foundation from the results of pore water pressure and that of the theoretical calculation, it shows that the simulation method of vertical strip drains presented in this paper is feasible and acceptable. The comparison of the model test results with that of theoretical calculation indicates that the strip drain simulation method described in this paper is acceptable.
- vertical strip drains /
- centrifugal model test /
- soft foundation /
- consolidation

HTML全文

图 1 模型断面及传感器布置

Figure 1. The model section and the sensor location

下载: 全尺寸图片幻灯片

图 2 第一级试验模型表面沉降

Figure 2. The surface settlement of the model in the first load

下载: 全尺寸图片幻灯片

图 3 模型表面沉降

Figure 3. The surface settlement of the model

下载: 全尺寸图片幻灯片

图 4 第二级加载表面沉降-时间关系(原型)

Figure 4. The surface settlement-time relationship (prototype)

下载: 全尺寸图片幻灯片

图 5 第一级加载孔压变化

Figure 5. Change of pore water pressure in the first load

下载: 全尺寸图片幻灯片

图 6 第二级加载孔压变化

Figure 6. Change of pore water pressure in the second load

下载: 全尺寸图片幻灯片

图 7 地基固结度随时间变化

Figure 7. The change of consolidation of the foundation over time

下载: 全尺寸图片幻灯片

图 8 断面加荷速率

Figure 8. The loading rate of the section

下载: 全尺寸图片幻灯片

表 1 地基层物理力学性质指标

Table 1. The physical and mechanical indexes of foundation

地基层	w/%	γ/(kN·m^-3)		e₀	G_s	C_v/ (cm²·s^-1)	C_h/ (cm²·s^-1)	C/ kPa	φ/ (°)	E_s/ MPa
地基层	w/%	湿	干	e₀	G_s	C_v/ (cm²·s^-1)	C_h/ (cm²·s^-1)	C/ kPa	φ/ (°)	E_s/ MPa
淤泥层	55.1	16.9	11.1	1.53	2.71	0.52e-3	0.55e-3	11.1	13	2.27
粉细砂层	19.6	20.6	17.3	0.56	2.69	3.06e-3	—	—	—	6.22
注：w—含水率；γ—重度；e₀—孔隙比；G_s—土粒比重；C_v—竖向固结系数；C_h—水平固结系数；C—固结快剪试验粘聚力；φ—固结快剪试验内摩擦角；E_s—压缩模量

下载: 导出CSV

表 2 离心机分级加载运行时间

Table 2. The stepping loading time of the centrifuge

分级	原型加荷开始时间/d	原型加荷时间间隔/d	模型100g稳定时间/min
第一级	0	200	28.8
第二级	200	80	11.5
加载两年	280	450	64.8

下载: 导出CSV

表 3 分级加载时地基沉降(原型)

Table 3. The settlement of the foundation in the step loading (prototype)

测点	第一级加载				第二级加载及运行期
测点	第一级施工期沉降/m	第一级结束时沉降/m	第一级开始10 d 平均沉降速率/ (mm·d^-1)	第一级最后10 d 平均沉降速率/ (mm·d^-1)	第二级开始10 d 平均沉降速率/ (mm·d^-1)	最后10 d 平均沉降速率/ (mm·d^-1)	加载2 a时沉降/m
LS1	0.81	1.32	9.19	0.35	4.29	0.29	1.97
LS2	1.39	2.08	12.58	0.68	4.71	0.29	2.72
LS3	1.15	1.82	12.26	0.61	3.99	0.34	2.36

下载: 导出CSV

表 4 孔压统计表(原型)

Table 4. The statistical table of the pore water pressure (prototype)

传感器编号	加载高度(原型)			孔隙水压力/kPa
传感器编号	第一级/m	第二级/m	u₀	u_max	u_t=0	u_t=200	u_t=280	u_t=730
2-1	4.5	15.0	153	388	212	184	356	218
2-2	13.0	15.0	153	360	277	251	331	194
2-3	10.4	10.4	153	283	241	220	232	184
2-4	5.4	5.4	153	240	221	204	215	177

下载: 导出CSV

表 5 运行两年时U_p

Table 5. The degree of consolidation in the operating period of two years

传感器编号	U_p/%
2-1	72.3
2-2	80.1
2-3	76.2
2-4	72.4

下载: 导出CSV

表 6 各加载阶段软土地基U_rz

Table 6. The degree of consolidation of the soft soil foundation in each loading stage

加载阶段	原型时间/d	U_rz(不考虑井阻、涂抹效应)/%	U_rz(考虑井阻、涂抹效应)/%
第一级加载开始	0	0	0
第二级加载开始	200	39.2	25.3
第二级加载完成	280	67.0	44.9
加载完运行两年	730	97.9	81.0

下载: 导出CSV

参考文献(16)

[1]	侯瑜京, 韩连兵, 梁建辉.深水港码头围堤和群桩结构的离心模型试验[J].岩土工程学报, 2004, 26(5):594~600 http://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200405003.htm HOU Yu-jing, HAN Lian-bing, LIANG Jian-hui. Centrifuge modeling of sea dike and pile groups in a harbor[J].Chinese Journal of Geotechnical Engineering, 2004, 26(5):594~600. http://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200405003.htm
[2]	包承纲, 蔡正银, 陈云敏, 等.岩土离心模拟技术的原理和工程应用[M].武汉:长江出版社, 2011 BAO Cheng-gang, CAI Zheng-yin, CHEN Yun-min, et al. The principle and engineering application of geotechnical centrifuge modeling technology[M]. Wuhan:The Changjiang Press, 2011.
[3]	Sharma J S, Bolton M D. Centrifugal and numerical modeling of reinforced embankments on soft clay installed with wick drains[J]. Geotextiles and Geomembranes, 2001, 19:23~44. doi: 10.1016/S0266-1144(00)00009-1
[4]	卢国胜.塑料排水板处理软基的离心机试验研究[J].西南科技大学学报, 2006, 21(4):43~45 http://www.cnki.com.cn/Article/CJFDTOTAL-XNGX200604009.htm LU Guo-sheng. Centrifuge Experiment to Improve Soft Foundation through Plastic Wick Drain[J]. Journal of Southwest University of Science and Technology, 2006, 21(4): 43~45. http://www.cnki.com.cn/Article/CJFDTOTAL-XNGX200604009.htm
[5]	饶锡保, 龚壁卫, 程展林, 等. 基于离心模型试验的某公路软基沉降变形规律研究[C] //中国水利学会2007学术年会论文集: 物理模拟技术在岩土工程中的应用. 苏州: 中国水利学会, 2007: 119~125 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGSL200710004020.htm RAO Xi-bao, GONG Bi-wei, CHENG Zhan-lin, et al. The Research of Settlement Deformation Law of a Certain Highway Soft Foundation Based on the Centrifugal Model Test[C] //The monograph of academic annual conference held by Chinese Hydraulic Engineering Society in 2007: Physical simulation technology application in geotechnical engineering. Suzhou: Chinese Hydraulic Engineering Society, 2007: 119~125. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGSL200710004020.htm
[6]	蒋关鲁, 胡润忠, 李安洪.离心模型试验预测中等压缩性土地基沉降的可行性[J].交通运输工程学报, 2011, 11(6):18~23 http://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201106006.htm JIANG Guan-lu, HU Run-zhong, LI An-hong. Feasibility of predicting settlement of medium compression soil foundation with centrifuge model test[J].Journal of Traffic and Transportation Engineering, 2011, 11(6):18~23. http://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201106006.htm
[7]	陈胜立, 张建民, 张丙印, 等.软土地基上土工织物加筋堤的离心模型试验研究[J].岩土力学, 2006, 27(5):804~806 http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200605025.htm CHEN Sheng-li, ZHANG Jian-min, ZHANG Bing-yin, et al. Numerical Simulation of Centrifugal Model Test on Reinforced Embankment with Lime-stabilized Soil as Backfill On Soft Clay Foundation[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 27(5):804~806. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200605025.htm
[8]	侯瑜京.离心模型试验模拟塑料排水板处理软基的试验研究[J].大坝观测与土工测试, 1995, 19(5):18~20 http://www.cnki.com.cn/Article/CJFDTOTAL-DBGC505.003.htm HOU Yu-jing. Centrifugal Modeling of The Plastic Plank in Soft Foundation Treatment[J].Dam Observation and Geotechnical Tests, 1995, 19(5):18~20. http://www.cnki.com.cn/Article/CJFDTOTAL-DBGC505.003.htm
[9]	高长胜, 张凌, 汪肇京, 等.塑料排水板的等效直径[J].水利水运工程学报, 2002, 4:43~45 http://www.cnki.com.cn/Article/CJFDTOTAL-SLSY200204006.htm GAO Chang-sheng, ZHANG Ling, WANG Zhao-jing, et al. Equivalent diameter of prefabricated drain[J].HYDRO-SCIENCE AND ENGINEERING, 2002, 4:43~45. http://www.cnki.com.cn/Article/CJFDTOTAL-SLSY200204006.htm
[10]	BARRON R A. Consolidation of fine-grained soils by drain wells[J]. Transactions of the American Society of Civil Engineers, 1948, 113: 718~754. https://trid.trb.org/view.aspx?id=118608
[11]	孔德金, 苗中海.软基加固检测孔隙水压力分析[J].港工建设, 2000, 3:29~31 http://www.cnki.com.cn/Article/CJFDTOTAL-GAOG200003013.htm KONG De-jin, MIAO Zhong-hai. The Analysis on Variation of Pore Water Pressure during Consolidating Soft Soil Foundation[J].PORT ENGINEERING TECHNOLOGY, 2000, 3:29~31. http://www.cnki.com.cn/Article/CJFDTOTAL-GAOG200003013.htm
[12]	罗勇, 龚晓南, 连峰.成层地基固结性状中不同定义平均固结度研究分析[J].科技通报, 2006, 22(6):814~816 http://www.cnki.com.cn/Article/CJFDTOTAL-KJTB200606017.htm LUO Yong, GONG Xiao-nan, LIAN Feng. Comparable Analysis of Different Definitions of Average Degree of Consolidation of Layered Soils[J].BULLETIN OF SCIENCE AND TECHNOLOGY, 2006, 22(6):814~816. http://www.cnki.com.cn/Article/CJFDTOTAL-KJTB200606017.htm
[13]	程强, 顾立军, 冯伟骞.由实测沉降曲线推求最终沉降量计算方法的探讨[J].海河水利, 2010, 4:37~39 doi: 10.3969/j.issn.1004-7328.2010.04.015 CHENG Qiang, GU Li-jun, FENG Wei-jian. The Method of Calculating the Final Settlement by the Measured Settlement Curve[J].HAIHE WATER RESOUCES, 2010, 4:37~39. doi: 10.3969/j.issn.1004-7328.2010.04.015
[14]	姜远文, 吉随旺.由实测孔隙水压力数据推算软黏土的固结系数和固结度[J].路基工程, 2001, 2:26~29 doi: 10.3969/j.issn.1003-8825.2001.02.009 JIANG Yuan-wen, JI Sui-wang. The Calculation of the coefficient of consolidation and consolidation of soft clay by the measured pore water pressure[J].THE SUBGRADE ENGINEERING, 2001, 2:26~29. doi: 10.3969/j.issn.1003-8825.2001.02.009
[15]	钱晓丽, 张建勋, 陈为群.塑料排水板地基处理固结沉降特性[J].贵州大学学报(自然科学版), 2010, 27(3):92~94 http://www.cnki.com.cn/Article/CJFDTOTAL-GZDI201003024.htm QIAN Xiao-li, ZHANG Jian-xun, CHEN Wei-qun. Characteristics of Consolidation Settlement in Ground Treatment for Plastic Vertical Drain[J].Journal of Guizhou University(Natural Science), 2010, 27(3):92~94. http://www.cnki.com.cn/Article/CJFDTOTAL-GZDI201003024.htm
[16]	JTS. 147-1-2010, 港口工程地基规范[S]. JTS. 147-1-2010, Code for Foundation in Port Engineering[S]