Research of dynamic response patterns of high steep rock slope under earthquake effects
-
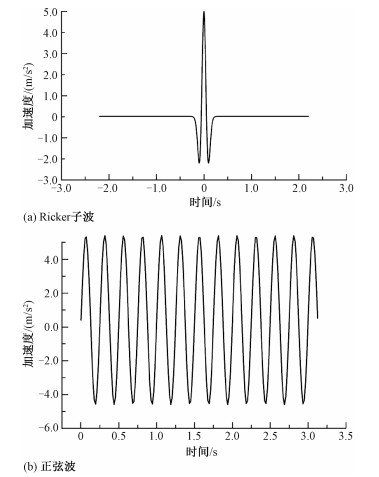
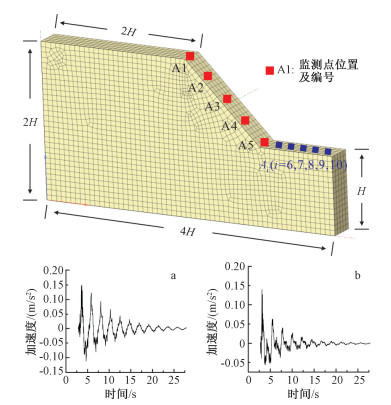
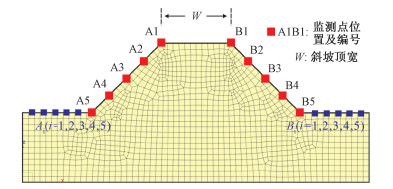
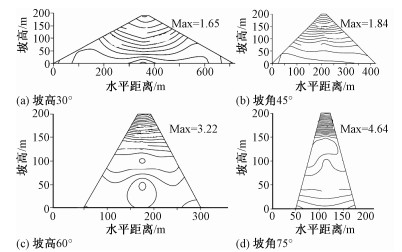
摘要: 在西南山区高陡单面斜坡研究基础上运用FLAC3D有限差分法对双面斜坡的动力响应规律进行分析，研究了斜坡坡高、坡角及顶宽变化对响应规律的影响，结果发现：对斜坡输入不同中心频率Ricker子波时，坡体卓越频率整体处于1~4 Hz之间，且斜坡不同部位卓越频率不尽相同。从规律上看，坡高决定了斜坡动力响应的表现形式，体现在坡高较低时加速度放大系数等值线平行于坡底而增大后变为平行于坡面展布的闭合区域，反映在放大效果上即为加速度随坡高线性增加（坡高较低时），而后呈现增减反复出现的情况（坡高较高时）；另外，坡角增大未影响斜坡动力响应的表现形式，仅改变了斜坡内部放大系数等值线的走向，使得陡倾斜坡加速度水平及竖向放大效果均大于缓倾斜坡。双面斜坡随坡形变化的动力响应规律与单面坡近乎相同，但由坡形改变所致地震波反射与折射现象使得双面坡对地震波的放大效果更加明显，表现为放大系数等值线密集程度增大，加速度较相同单面斜坡成倍增加。Abstract: Base on the research of single-sided high steep slopes in southwestern China, dynamic responses of double-sided slopes are analysed which include changes of height, angle and width. Results show that predominant frequencies of slopes mainly concentrate in 1~4 Hz when inputting Ricker waves with varying center frequencies and the results alter in different parts of the slope. Dynamic response patterns mainly depend on slope height, contours of amplification coefficients parallel to the bottom of slope at lower heights while distribute as closed regions near surface when height increases. This means numerical value of amplification linearly increase with the height of the slope at a relatively low height but fluctuate at a great height. In addition, slope angle changes the direction of contours and makes amplification factors greater in steep slope, but dynamic patterns of slope are unaffected by those changes. Double-sided slopes show similar dynamic pattern with the single ones, but reflection and refraction of quake waves caused by slope shape make the amplification greater in double-sided slopes, which manifest as intensified contours and multiplied acceleration.
-
Key words:
- earthquake /
- high steep rock slopes /
- topography /
- dynamic response /
- amplification effect /
- numerical simulation
-
图 1 计算选用的斜坡模型尺寸及边界条件设置
H—坡高；α—坡度
Figure 1. Scales and boundary conditions of the slope model
图 2 计算选用的Ricker子波与正弦地震波
Figure 2. Ricker wavelet and sinusoidal seimic wave for calculation
图 3 斜坡计算模型设置及加速度记录
a—坡肩(A1)加速度时程记录；b—坡脚(A5)加速度时程记录
Figure 3. The calculation model and acceleration records of the slope
图 4 Ricker波作用下斜坡坡面加速度监测曲线
Figure 4. Monitoring curves of the slope surface acceleration under the action of Ricker wave
图 5 不同高度斜坡加速度放大系数等值线图
Max-加速度放大系数最大值
Figure 5. Contours of slope acceleration amplification coefficients with different slope heights
图 6 高陡斜坡不同位置加速度放大系数拟合曲线
Figure 6. Fitting curves of acceleration amplification coefficients in different places of the high steep slope
图 7 不同坡角下高陡斜坡加速度放大系数等值线图
Figure 7. Contours of acceleration amplification coefficients at different angles of the high steep slopes
图 8 双面高陡斜坡计算模型及监测点布置
Figure 8. The model and monitoring points of the double-sided high steep slope
图 9 不同坡高及顶宽双面斜坡加速度放大系数等值线图
Figure 9. Contours of acceleration amplification coefficients of double-sided slopes with different heights and widths
图 10 不同坡角双面斜坡加速度放大系数等值线图
Figure 10. Contours of acceleration amplification factors of double-sided slopes with different angles
图 11 双面及单面斜坡加速度放大系数随坡角变化拟合曲线
Figure 11. Fitting curves of acceleration amplification coefficients with the change of slope angles of double and single-sided slopes
图 12 坡面加速度放大系数随顶宽变化拟合曲线(以坡高200 m为例)
Figure 12. Fitting curves of acceleration amplification coefficients with the change of crest widths of slope surface(Taking 200 m slope as an example)
表 1 岩质斜坡计算选用的物理力学参数(据王文沛等，2019)
Table 1. Physical and mechanical parameters for the rock slope (Wang et al., 2019)
密度ρ/
(kg·m-3)体积模量
G/GPa剪切模量
G/GPa内摩擦角
φ/(°)粘聚力
C/MPa抗拉强度
Rm/MPa2690 23.3 14 40 1.8 5.56 
下载: 导出CSV
-
ASHFORD S A, SITA N, LYSMER J, et al., 1997. Topographic Effects on the Seismic Response of Steep Slopes[J]. Bulletin of the Seismological Society of America, 87(3):701-709. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3b8337d859577f0ff6432657894174ef BOORE D M, 1972. A note on the effect of simple topography on seismic SH waves[J]. Bulletin of the Seismological Society of America, 62(1):275-284. http://cn.bing.com/academic/profile?id=fe8421b116e9ea2d5fe278a05248621b&encoded=0&v=paper_preview&mkt=zh-cn BOURDEAU C, HAVENITH H B, 2008. Site effects modelling applied to the slope affected by the Suusamyr earthquake (Kyrgyzstan, 1992)[J]. Engineering Geology, 97(3-4):126-145. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=82430ffa57225b14c4dc880d4d01a6fc ÇELEBI M, 1987. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake[J]. Bulletin of the Seismological Society of America, 77(4):1147-1167. http://cn.bing.com/academic/profile?id=a77bd29b8f7b826b3e109b7b25a23e8e&encoded=0&v=paper_preview&mkt=zh-cn DI FIORE V. 2010. Seismic site amplification induced by topographic irregularity:results of a numerical analysis on 2D synthetic models[J]. Engineering Geology, 114(3-4):109-115. http://cn.bing.com/academic/profile?id=8817cf3e853aaad1cf5dd4efb1fe22f5&encoded=0&v=paper_preview&mkt=zh-cn GELI L, BARD P Y, JULLIEN B, 1998. The effect of topography on earthquake ground motion:a review and new results[J]. Bulletin of the Seismological Society of America, 78(1):42-63. http://cn.bing.com/academic/profile?id=18827fe4fe518f5a10c3912b0a88d125&encoded=0&v=paper_preview&mkt=zh-cn GUO X B, XIAO Z X, ZHANG Z C, 2001. Slope effect of blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 20(1):83-87. (in Chinese with English abstract) http://d.old.wanfangdata.com.cn/Periodical/zdycj201801037 HARP E L, JIBSON R W, 2002. Anomalous concentrations of seismically triggered rock falls in Pacoima canyon:are they caused by highly susceptible slopes or local amplification of seismic shaking?[J]. Bulletin of the Seismological Society of America, 92(8):3180-3189. http://cn.bing.com/academic/profile?id=e392084e3f26e7ae51ccbc13d3f45716&encoded=0&v=paper_preview&mkt=zh-cn HE Y L, LU S Y, 1998. A method for calculating the seismic action in rock slope[J]. Chinese Journal of Geotechnical Engineering, 20(2):66-68. (in Chinese with English abstract). HE Y L, LU S Y, DUAN Y H, 1998. Seismic response analysis of gravity dam[J]. World Information on Earthquake Engineering, 14(3):32-36. (in Chinese with English abstract) http://d.old.wanfangdata.com.cn/Periodical/slxb201911005 Itasca Consulting Group Inc., 2005. FLAC (fast Lagrange analysis of continua) slope user's guide (Version 5.0)[Z]. Minneapolis, USA: Itasca Consulting Group Inc. LI N, WANG B Q, MEN Y M, et al., 2018. Study on dynamic response of landslide supported by pressure-type anchor under earthquake[J]. Journal of Geomechanics, 24(4):490-497. (in Chinese with English abstract) http://d.old.wanfangdata.com.cn/Periodical/dzlxxb201804006 LUO Y H, 2011. Study on complex slopes response law under earthquake action[D]. Chengdu: Chengdu University of Technology. (in Chinese with English abstract) LYSMER J, KUHLEMEYER R L, 1969. Finite dynamic model for infinite media[J]. Journal of the Engineering Mechanics Division, 95(4):859-878. http://cn.bing.com/academic/profile?id=e19d042440e31a34cced83ad3d79da01&encoded=0&v=paper_preview&mkt=zh-cn MEUNIER P, HOVIUS N, HAINES A J, 2007. Regional patterns of earthquake-triggered landslides and their relation to ground motion[J]. Geophysical Research Letters, 34(20):L20408. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=41ffb1fc56da83809371b3ffbd3c20d4 MITANI Y, WANG F W, OKEKE A C, et al., 2013. Dynamic analysis of earthquake amplification effect of slopes in different topographic and geological conditions by using ABAQUS[M]//WANG F W, MIYAJIMA M, LI T D, et al. Progress of Geo-Disaster Mitigation Technology in Asia. Berlin: Springer, 469-489. PARISE M, JIBSON R W, 2000. A seismic landslide susceptibility rating of geologic units based on analysis of characteristics of landslides triggered by the 17 January, 1994 Northridge, California earthquake[J]. Engineering Geology, 58(3-4):251-270. http://cn.bing.com/academic/profile?id=cc6b160106478c22a0062dcf0af29f36&encoded=0&v=paper_preview&mkt=zh-cn QI S W, 2006. Two patterns of dynamic responses of single-free-surface slopes and their threshold height[J]. Chinese Journal of Geophysics, 49(2):518-523. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb200602026 QI S W, WU F Q, SUN J Z, 2003. General regularity of dynamic responses of slopes under dynamic input[J]. Science in China Series E Technological Sciences, 33(S1):28-40. (in Chinese) http://cn.bing.com/academic/profile?id=09364f028d5db23ce6a88c12efaf4d16&encoded=0&v=paper_preview&mkt=zh-cn WANG H Y, XIE L L, 2010. Effects of topography on ground motion in the Xishan park, Zigong city[J]. Chinese Journal of Geophysics, 53(7):1631-1638. (in Chinese with English abstract) http://cn.bing.com/academic/profile?id=2252b8f5c4d67a88873fcadc13649a8d&encoded=0&v=paper_preview&mkt=zh-cn WANG W P, LI B, FENG Z, et al., 2019. Failure mechanism of a high-steep rock slope considering site effect[J]. Rock and Soil Mechanics, 40(1):297-304, 314. (in Chinese with English abstract) http://d.old.wanfangdata.com.cn/Periodical/ytlx201901030 WANG W P, YIN Y P, LI B, et al., 2015. Spectral characteristics of dynamic response of slope with different angles of inclination[J]. Chinese Journal of Rock Mechanics and Engineering, 34(1):121-128. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201501014 YANG G X, WU F Q, DONG J Y, et al., 2012. Study of dynamic response characters and failure mechanism of rock slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 31(4):696-702. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201204007 YIN Y P, 2008. Researches on the geo-hazards triggered by Wenchuan earthquake, Sichuan[J]. Journal of Engineering Geology, 16(4):433-444. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcdzxb200804001 YIN Y P, WANG W P, 2014. Researches on seismic landslide stability analysis[J]. Journal of Engineering Geology, 22(4):586-600. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcdzxb201404007 ZHANG D, WU Z H, LI J C, et al., 2013. An overview on earthquake-induced landslide research[J]. Journal of Geomechanics, 19(3):225-241. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzlxxb201303001 ZHANG Y S, LEI W Z, SHI J S, et al., 2008. General characteristics of 5.12 earthquake-induced geohazards in Sichuan[J]. Journal of Geomechanics, 14(2):109-119. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzlxxb200802002 ZHOU X T, HAN J L, SHI F G, et al., 2014. Numerical simulation for amplification effect of topography and geomorphology to seismic waves[J]. Journal of Engineering Geology, 22(6):1211-1220. (in Chinese with English abstract) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcdzxb201406027 郭学彬, 肖正学, 张志呈. 2001.爆破振动作用的坡面效应[J].岩石力学与工程学报, 20(1):83-87. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200101019 何蕴龙, 陆述远, 1998.岩石边坡地震作用近似计算方法[J].岩土工程学报, 20(2):66-68. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199800687336 何蕴龙, 陆述远, 段亚辉, 1998.重力坝地震动力响应分析[J].世界地震工程, 14(3):32-36. http://www.cnki.com.cn/Article/CJFDTotal-SJDC803.005.htm 李楠, 汪班桥, 门玉明, 等, 2018.压力型锚杆支护滑坡的地震动力响应特性研究[J].地质力学学报, 24(4):490-497. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20180406&journal_id=dzlxxb 罗永红, 2011.地震作用下复杂斜坡响应规律研究[D].成都: 成都理工大学. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1959647 祁生文, 伍法权, 孙进忠, 2003.边坡动力响应规律研究[J].中国科学E辑技术科学, 33(S1):28-40. http://www.cnki.com.cn/Article/CJFDTotal-JEXK2003S1003.htm 祁生文, 2006.单面边坡的两种动力反应形式及其临界高度[J].地球物理学报, 49(2):518-523. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb200602026 王海云, 谢礼立, 2010.自贡市西山公园地形对地震动的影响[J].地球物理学报, 53(7):1631-1638. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201007014 王文沛, 殷跃平, 李滨, 等, 2015.不同坡角斜坡动力响应频谱特征研究[J].岩石力学与工程学报, 34(1):121-128. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201501014 王文沛, 李滨, 冯振, 等, 2019.考虑场地效应的高陡岩质斜坡地震失稳机制[J].岩土力学, 40(1):297-304, 314. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytlx201901030 杨国香, 伍法权, 董金玉, 等, 2012.地震作用下岩质边坡动力响应特性及变形破坏机制研究[J].岩石力学与工程学报, 31(4):696-702. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201204007 殷跃平, 2008.汶川八级地震地质灾害研究[J].工程地质学报, 16(4):433-444. http://d.old.wanfangdata.com.cn/Periodical/gcdzxb200804001 殷跃平, 王文沛, 2014.论滑坡地震力[J].工程地质学报, 22(4):586-600. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcdzxb201404007 张铎, 吴中海, 李家存, 等, 2013.国内外地震滑坡研究综述[J].地质力学学报, 19(3):225-241. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20130301&journal_id=dzlxxb 张永双, 雷伟志, 石菊松, 等, 2008.四川5.12地震次生地质灾害的基本特征初析[J].地质力学学报, 14(2):109-116. http://journal.geomech.ac.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20080202&journal_id=dzlxxb 周兴涛, 韩金良, 施凤根, 等, 2014.地形地貌对地震波放大效应数值模拟研究[J].工程地质学报, 22(6):1211-1220. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcdzxb201406027 -
下载:
计量
- 文章访问数: 440
- HTML全文浏览量: 185
- PDF下载量: 23
- 被引次数: 0
