STRENGTH ESTIMATION OF COLUMNAR JOINTED BASALTIC MASS BASED ON GEOLOGICAL STRENGTH INDEX
-
摘要: 节理岩体的强度是岩体工程设计的重要参数, 柱状节理岩体作为一种具有柱状镶嵌结构的特殊节理岩体, 缺乏相似的工程案例, 其岩体强度的确定是目前水电工程中的热点问题。本文综述了国内外相似工程中柱状节理岩体强度的研究进展, 以白鹤滩水电工程为例, 结合Hoek和Brown最新提出的地质强度指标法和强度准则估算了不同爆破损伤下的柱状镶嵌块状结构和柱状镶嵌碎裂结构柱状节理岩体的强度参数, 并得到白鹤滩水电站的原位试验成果的验证, 计算表明基于地质强度指标法的Hoek和Brown强度准则能较好的反映柱状节理岩体的强度参数。
-
关键词:
- 柱状节理 /
- 岩体强度 /
- 地质强度指标法 /
- Hock-Brown强度准则
Abstract: The strength parameters of jointed rock mass are important to rock engineering design.The columnar jointed basaltic mass is special with columnar mosaic structure and the similar engineering case la cks.The strength of columnar jointed basaltic mass currently becomes an advanced research hotspot in hydropower project.This paper reviews domestic and international researches on strength of columnar jointed basaltic mass.Taking the columnar jointed basaltic at Baihetan Hydropower Station as an example, the GSI and Hoek-Brown Criterion are applied to estimate strength parameters of columnar mosaic blocky and cataclastic basaltic masses under different blasting damages.The result is proved by in situ tests at Baihetan Hydropower Station.It is concluded that the GSI-based Hoek-Brown Criterion can better reflect real strength parameters of columnar jointed basaltic masses. -
0. 引言
节理岩体的强度是岩体工程设计的重要参数, 柱状节理岩体作为一种具有柱状镶嵌结构的特殊节理岩体, 普遍发育于玄武岩中, 构成著名地质景观, 如图 1所示, 近年来逐渐作为水电工程的坝基岩体, 由于柱状节理在岩体中高密度发育, 对岩体强度的影响是工程中重点关注的问题。以往一般采用试验和理论的方法获取节理岩体的强度参数, 虽然原位试验是研究岩体强度的最直接方法, 但对柱状节理岩体而言, 匮乏相似的工程案例, 原位试验也不易进行, 而从现有的理论强度准则去揭示复杂节理岩体的强度特性, 或太多简化, 或公式复杂难以应用。因此, 如何利用现有地质信息及小型标准试样的室内试验资料, 对柱状节理岩体的宏观强度做出方便可靠的预测变得尤为重要。
自上世纪八十年代以来, Hoek和Brown发展了一种评价岩体强度参数的新方法———地质强度指标(Geological Strength Index, 简称GSI), 见Hoek和Brown (1980[1]和1988[2]), Hoek等(2002[3]), Hoek和Diederichs (2006[4]), Hoek和Marinos (2007[5])。广义Hoek-Brown经验准则认为:岩体质量的评定和岩体抗剪强度参数的确定是可以区分开的, 通过工程地质人员用定量指标合理地描述岩体的岩性、结构和不连续面条件等因素, 评价各种地质条件对岩体强度削弱程度, 对岩体质量进行量化评分和分级, 然后利用岩体质量指标值与岩体变形模量之间的经验关系来合理地描述岩体的强度参数。
从现有的文献上看, 国外在建筑工程、环境工程及核工程中已经成功地应用GSI法评估了柱状节理岩体的工程力学特性。Justo (2006)[6]采用GSI法评价了Tenerife Island的一座高达40层楼房的节理玄武岩地基的变形参数及强度参数。Schultz (1995)[7]采用GSI法合理估计了美国汉佛柱状节理岩体核废料储存工程(Basalt waste isolation project, 简称BWIP)的柱状节理岩体的强度参数, 但应用在国内水利工程柱状节理岩体强度评价中则较为少见。本文以白鹤滩水电工程为例, 结合最新的GSI法和Hoek-Brown强度准则对柱状节理岩体强度进行估算。
2. 白鹤滩水电站柱状节理岩体特征
白鹤滩水电站位于金沙江下游四川省宁南县和云南省巧家县境内, 上接乌东德梯级, 下邻溪洛渡梯级, 距离溪洛渡水电站195 km, 坝型为混凝土双曲拱坝, 坝高289m, 装机容量13050MW, 多年平均发电量584.84亿kW·h, 保证出力4335MW。是我国继三峡、溪洛渡之后开展前期工作的又一座千万千瓦级以上的水电站。白鹤滩水电站坝址区基岩以块状玄武岩为主, 地质构造相对简单, 具备修建高拱坝的地形地质条件。然而坝址区柱状节理发育, 岩心破碎, RQD值普遍较低, 完整性较差, 其强度指标相对较低, 尤其坝址区峨眉山玄武岩[8]第三层中部柱状节理密集发育, 柱体呈细长状, 柱面形状以五边形及四边形居多, 长度一般2 ~ 3m, 直径0.13 ~ 0.25m, 柱体平均倾角为15 ~ 25°, 节理线密度在13条m以上, 对拟建的白鹤滩双曲拱坝的变形、坝肩稳定、边坡稳定、地下洞室群围岩稳定都有一定的影响, 已成为该水电工程的主要岩石力学问题之一。
3. 柱状节理岩体强度的估算
Hoek等(2002)[3]修正的Hoek-Brown强度准则为:

(1) 式(1)中, σ1和σ3为岩体破坏时的最大和最小有效主应力, σci为完整岩块单轴抗压强度, mb、s和a为Hoek-Brown材料参数, 可查GSI表获取, 也可根据GSI值进行换算。S=1时代表完整岩块。D为岩体扰动因子, 其与爆破产生的损伤大小及岩体应力卸荷程度有关, 一般认为无扰动时为0, 部分扰动时为0.5, 严重扰动时为1。若由于小规模爆破导致岩体中等程度的破坏及应力释放引起某种岩体扰动, 当爆破良好时可取D=0.7, 爆破效果很差时取D=1.0;若由于大型生产爆破或者开挖上覆岩体而导致大型矿山边坡严重扰动时, 取D=1.0;软岩地区若采用撬挖或机械方式开挖, 边坡的破坏程度不高, 可取D=0.7。这里考虑开挖、爆破及施工等引起白鹤滩柱状节理岩体一定程度的扰动、损伤或破坏, 即D=0 ~ 1.0下岩体强度的变化区间。

(2) 
(3) 
(4) 令式(1)中的σ3和σ1分别等于0, 可得式(5)的岩体单轴抗压强度σc以及单轴抗拉强度σt。

(5) 至于抗剪强度参数, 则可以通过具有一定科学依据的经验准则来确定岩体质量指标值与岩体强度参数之间的经验关系。广义Hoek-Brown经验准则正是在基于大量原位资料及工程经验的基础上来确定岩体抗剪强度指标, 其所预测的强度包络线既符合室内对岩样所做三轴压缩试验, 又符合野外对节理岩体破坏的观察, 在工程应用中具有重要的意义。
由于大多数岩土软件中仍采用Mohr-Coulomb破坏准则, 因此很有必要建立Hoek-Brown破坏准则与Mohr-Coulomb破坏准则之间的联系, 由Hoek-Brown的最大和最小主应力关系曲线可以拟合得到等价的Mohr-Coulomb主应力关系直线, 其拟合得到的Mohr-Coulomb强度参数分别为:

(6) 
(7) 
(8) 
(9) 
(10) 
(11) 
(12) 式(10)和(11)中, σcm是等效Mohr-Coulomb破坏准则推求出的岩体抗压强度。σ3max是Hoek-Brown破坏准则与等效Mohr-Coulomb破坏准则围压上限值。H代表洞室埋深或边坡高度, 当地应力以水平方向最大时, 应用水平地应力代替γH。
由最大和最小主应力来表示法向应力和切向应力的公式为:

(13) 
(14) 
(15) 将等效Mohr-Coulomb破坏准则写成以最大和最小主应力表示的破坏准则为:

(16) 这里采用加拿大Rocscience公司开发的基于广义Hoek-Brown破坏准则的免费软件RocLab[9]来确定柱状节理岩体的强度参数及等效Mohr-Coulomb抗剪强度参数。根据白鹤滩柱状节理岩体的卸荷特征, 可分为柱状镶嵌块状结构和柱状镶嵌碎裂结构, 这里估算其在无扰动及爆破下的Hoek-Brown材料参数及抗剪强度参数。同时对比了Schultz (1995)采用GSI (1988)经验公式估算BWIP柱状节理玄武岩体的强度参数[7]。玄武岩体的材料参数mi为25 ±5, 这里采用美国能源部对BWIP柱状节理玄武岩体的试验值mi=22。σ3max的选取, 则根据白鹤滩河谷地应力场中柱状节理岩体位置处的小主应力的极大值估取。
由表 1整理的计算结果可知, 柱状镶嵌块状结构岩体的单轴抗压强度为14.00 ~ 25.00MPa, 单轴抗拉强度为0.30 ~ 0.64MPa; 爆破后的单轴抗压强度降低为4.00 ~ 11.00MPa, 单轴抗拉强度为0.01 ~ 0.35MPa。柱状镶嵌碎裂结构岩体的单轴抗压强度为2.50 ~ 4.60MPa, 单轴抗拉强度为0.04 ~ 0.08MPa; 爆破后的单轴抗压强度降低为0.50 ~ 1.10MPa, 单轴抗拉强度为0.01 ~ 0.03MPa。
表 1 基于GSI估算的白鹤滩水电站柱状节理玄武岩体强度Table 1. Strength parameters of columnar jointed basalt estimated by GSI at Baihetan hydropower station
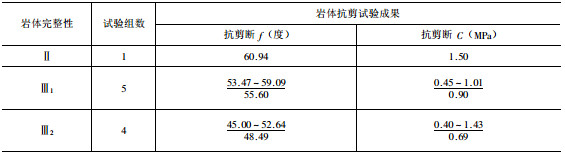
与摩尔—库仑强度包络线不同, Hoek-Brown破坏准则得到的强度包络线是一条非线性曲线, 其拟合的等效Mohr-Coulomb抗剪强度参数是与其围压有关。高围压下的岩体抗剪强度参数相应提高, 这与实际岩体揭示的情况相符。工程中普遍开展的直剪法试验, 在试验岩样制取时就无可避免地产生了一定程度的岩体扰动, 同时受试验条件限制无法考虑大尺度岩体及原岩应力, 在试验时仅单向受围压, 剪坏后则根据各剪切阶段特征点的剪应力和法向应力值, 并采用图解法或最小二乘法绘制剪应力与法向应力关系曲线并确定相应的摩尔—库仑抗剪强度参数。工程岩体实际剪破时的抗剪强度是考虑围压等多因素作用的强度, 因此直剪法试验其得到的岩体抗剪强度相对于Hoek-Brown破坏准则得到的强度参数偏低。比较中水顾问集团华东勘测设计研究院的现场岩体直剪试验①可知(表 2), 白鹤滩Ⅱ类岩体对应柱状镶嵌块状结构岩体, GSI法对摩擦角的估值接近现场直剪试验的值, 仅高出4.3 %, 凝聚力高出0.25 ~ 1.26MPa。现场岩体无Ⅳ类岩体直剪试验, Ⅲ1类岩体可视为产生一定卸荷松弛的Ⅱ类岩体即柱状镶嵌块状结构岩体。考虑爆破后的柱状镶嵌块状结构岩体GSI估值为:摩擦角53.4 ~ 57.66°, 凝聚力为0.90 ~ 1.54 MPa, 与Ⅲ1类岩体直剪试验成果相近。计算表明, 采用GSI估计柱状节理岩体的抗剪强度参数较为合理。
① 中水顾问集团华东勘测设计研究院.金沙江白鹤滩水电站柱状节理玄武岩工程地质研究报告[R].杭州, 2006.
表 2 岩体抗剪断试验成果Table 2. Shear test results of rock mass
4. 结论
本文综述了基于GSI法的广义Hoek-Brown破坏准则在国内外柱状节理岩体强度估值中的应用, 并将该法应用于白鹤滩水电工程中, 估算了柱状镶嵌块状结构和柱状镶嵌碎裂结构的柱状节理玄武岩体的变形模量及强度参数, 并考虑了扰动岩体、不同爆破损伤岩体的变形模量及强度参数, 计算表明:
(1) 广义Hoek-Brown破坏准则是基于大量原位资料及工程经验的经验准则, 其所预测的柱状节理岩体变形模量及强度参数, 与白鹤滩水电站工程原位试验成果较为一致, 参数估值合理, 可以应用于类似的工程中。
(2) Hoek-Brown破坏准则得到的强度包络线为非线性曲线, 其拟合的等效Mohr-Coulomb抗剪强度参数是与围压有关, 能够更合理地描述不同应力状态下的岩体强度参数。
-
表 1 基于GSI估算的白鹤滩水电站柱状节理玄武岩体强度
Table 1. Strength parameters of columnar jointed basalt estimated by GSI at Baihetan hydropower station
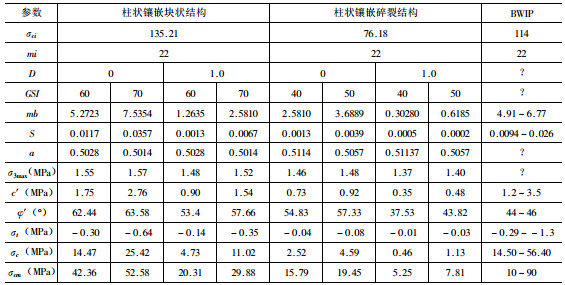
表 2 岩体抗剪断试验成果
Table 2. Shear test results of rock mass
-
[1] Hoek E, Brown E T.Underground Excavations in Rock[M].London:Institution of Mining and M etallurgy, 1980. [2] Hoek E, Brown E T. The Hoek-Brown failure criterion-a 1988 update[A]. Proc. 15th Canadian Rock Mech. Symp. (ed. J. H. Curran), pp. 31 ~ 38. Toronto : Civil Engineering Dept, University of Toronto, 1988. [3] Hoek E, CarranzaTorres C T, Corkum B. Hoek-Brown failure criterion-2002 edition[A]. Proc. North American Rock Mechanics Society Meeting, Toronto, 2002. [4] Hoek E, Diederichs M S.Empirical estimation of rock mass modulus[J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43 (2):203 ~ 215. doi: 10.1016/j.ijrmms.2005.06.005 [5] Hoek E, Marinos P.A brief history of the development of the Hoek-Brown failure criterion[J].Soils and Rocks, 2007 (2):1 ~ 13. https://www.mendeley.com/research-papers/brief-history-development-hoekbrown-failure-criterion-2/ [6] Justo J L, Justo E, Durand P, et al.The foundation of a 40-storey tower in jointed basalt[J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43 (2):267. doi: 10.1016/j.ijrmms.2005.07.007 [7] Schultz R A.Limits on strength and deformation properties of jointed basaltic rock masses[J].Rock Mechanics and Rock Engineering, 1995, 28 (1):1 ~ 15. http://cn.bing.com/academic/profile?id=8d169ff6318bc78701d400b05851ae57&encoded=0&v=paper_preview&mkt=zh-cn [8] 沈军辉, 王兰生.峨眉山玄武岩的岩相与岩体结构[J].水文地质工程地质, 2001, 28 (6):1 ~ 4. http://d.old.wanfangdata.com.cn/Periodical/swdzgcdz200106001Shen Jun-hui, Wang Lan-sheng.The lithofacies and the rock mass structure of Emei Mountain basalt rockmass[J]. Hydrogeology and Engineering Geology, 2001, 28 (6):1 ~ 4 (in Chinese). http://d.old.wanfangdata.com.cn/Periodical/swdzgcdz200106001 [9] Hoek E, Users's Guide of Roclab-Strength analysis of rock and soil masses by using the Hoek-Brown, Mohr-Coulomb failure criteria[M]. Rocscience Inc, 2003. -






 下载:
下载:

 下载:
下载:


