图  2  相场演化原理示意图

a—混合型断裂示意图；b—I 型断裂驱动力示意图；c—II 型断裂驱动力示意图；d—I–II 混合型断裂驱动力示意图

Figure  2.  Schematics of the phase-field evolution principles (a) Mixed-mode fracture; (b) Mode-I fracture driving forces; (c) Mode-II fracture driving force; (d) Mixed mode I-II fracture driving forces

图  1  具有特征长度$ \ell _{c} $的弥散损伤区$ {\varGamma }_{\ell _{c}} $在相场法示意图

Figure  1.  Schematic diagram of phase–field method for a diffuse damage zone with a characteristic length

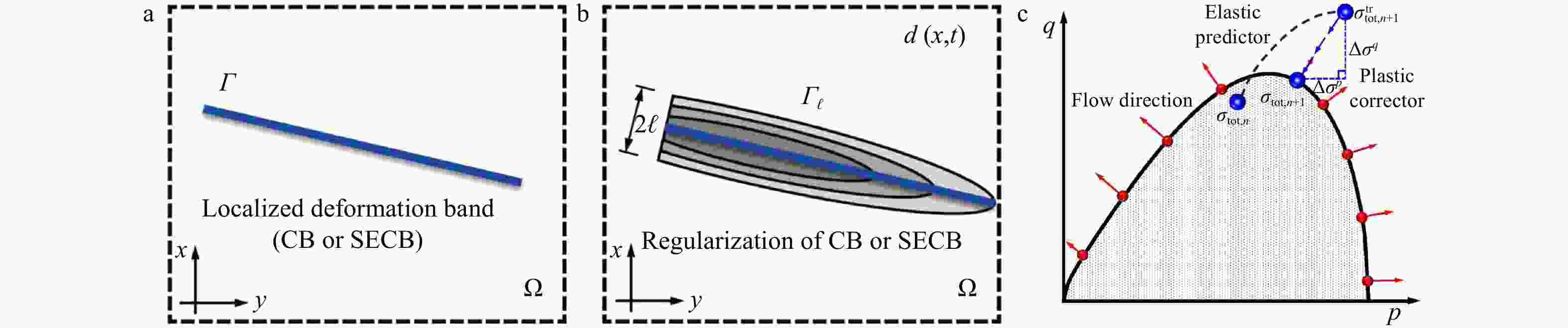
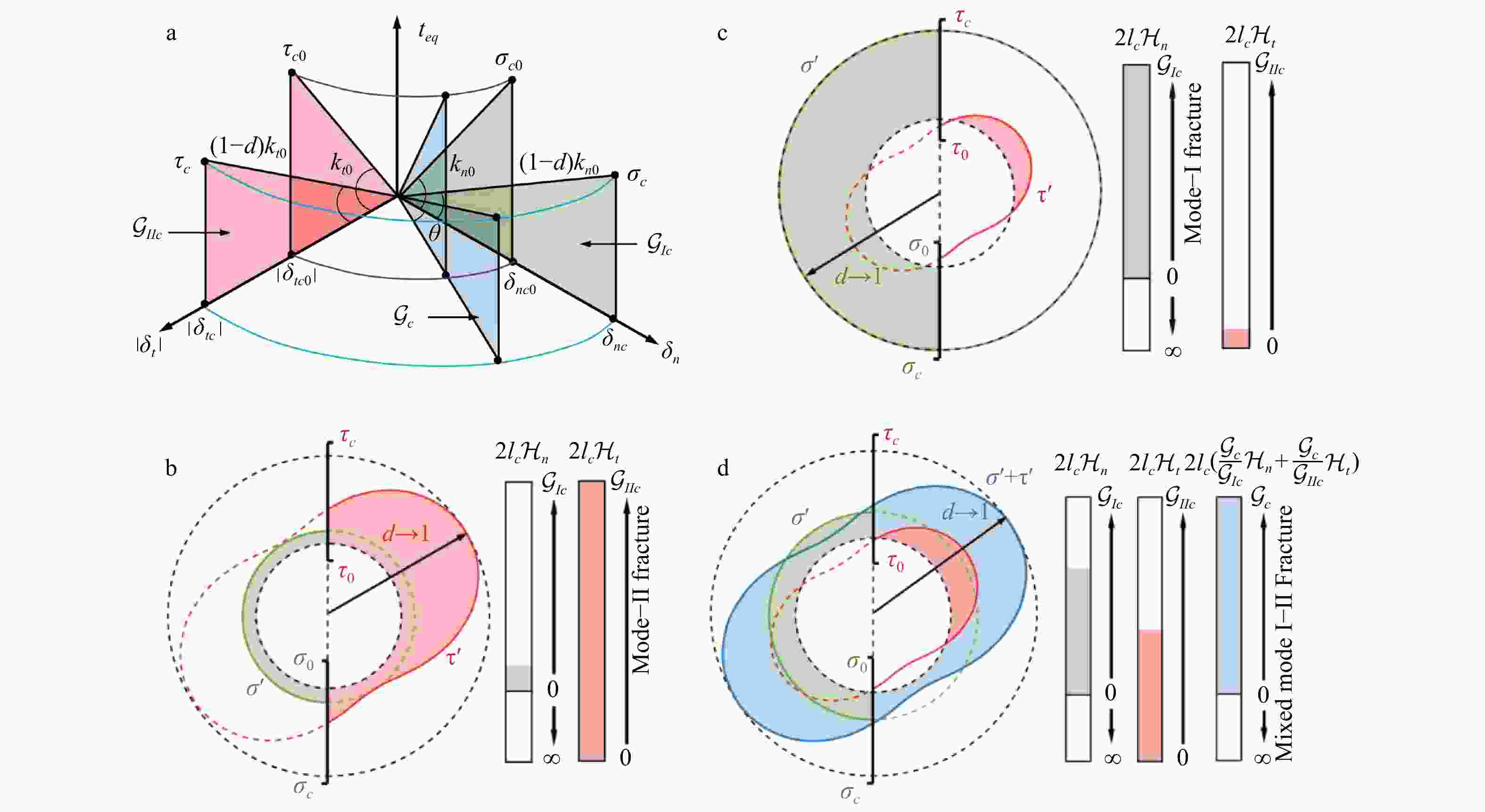
图  3  应变损伤局部化的相场示意图

a—局部化带的尖锐拓扑结构；b—相场正则化变形带；c—不同围压下的流动方向示意图及其广义回归映射几何解释

Figure  3.  Phase–field schematics of strain localization

(a) Sharp topology of localization zones; (b) The relevant phase–field regularized deformation bands; (c) Schematics of flow directions at different confining pressures and the general return mapping geometric interpretation

图  4  含单条预制裂隙和3条预制裂隙的类岩试样在单轴压缩试验中的几何形状及边界条件

Figure  4.  Geometry and boundary conditions of fissured rock-like specimens in the uniaxial compression tests: a single preexisting fissure and three preexisting fissures

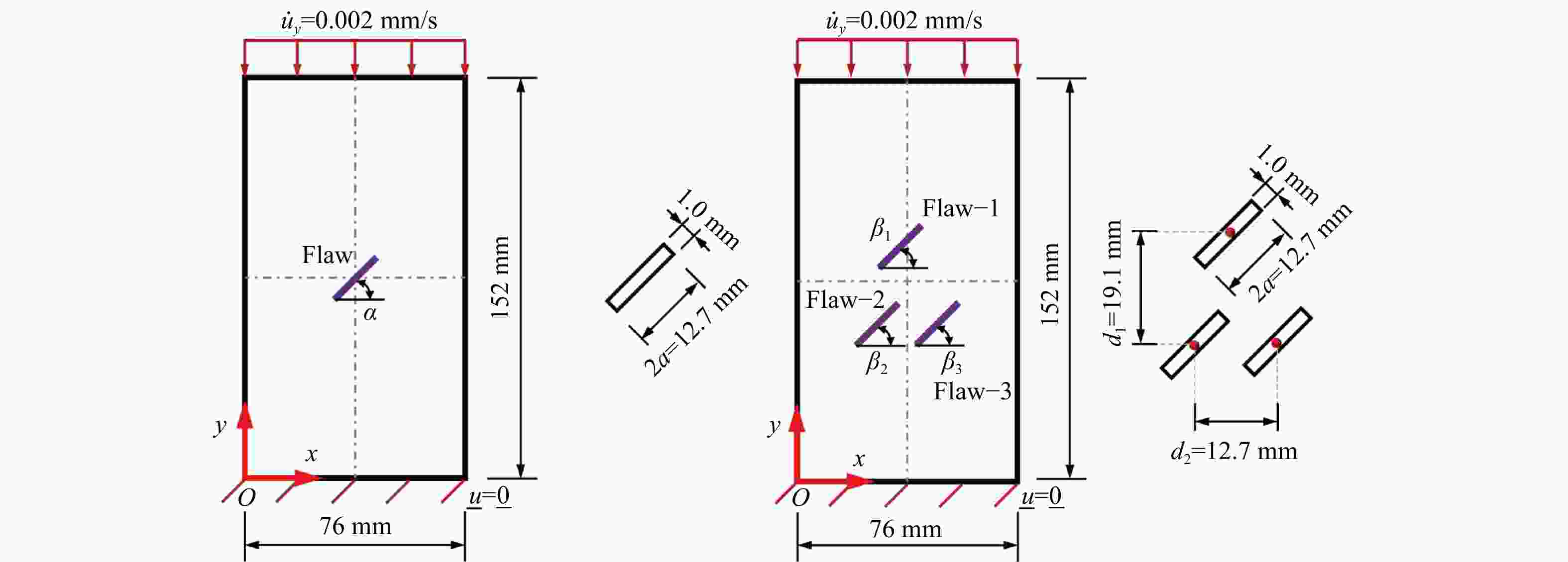
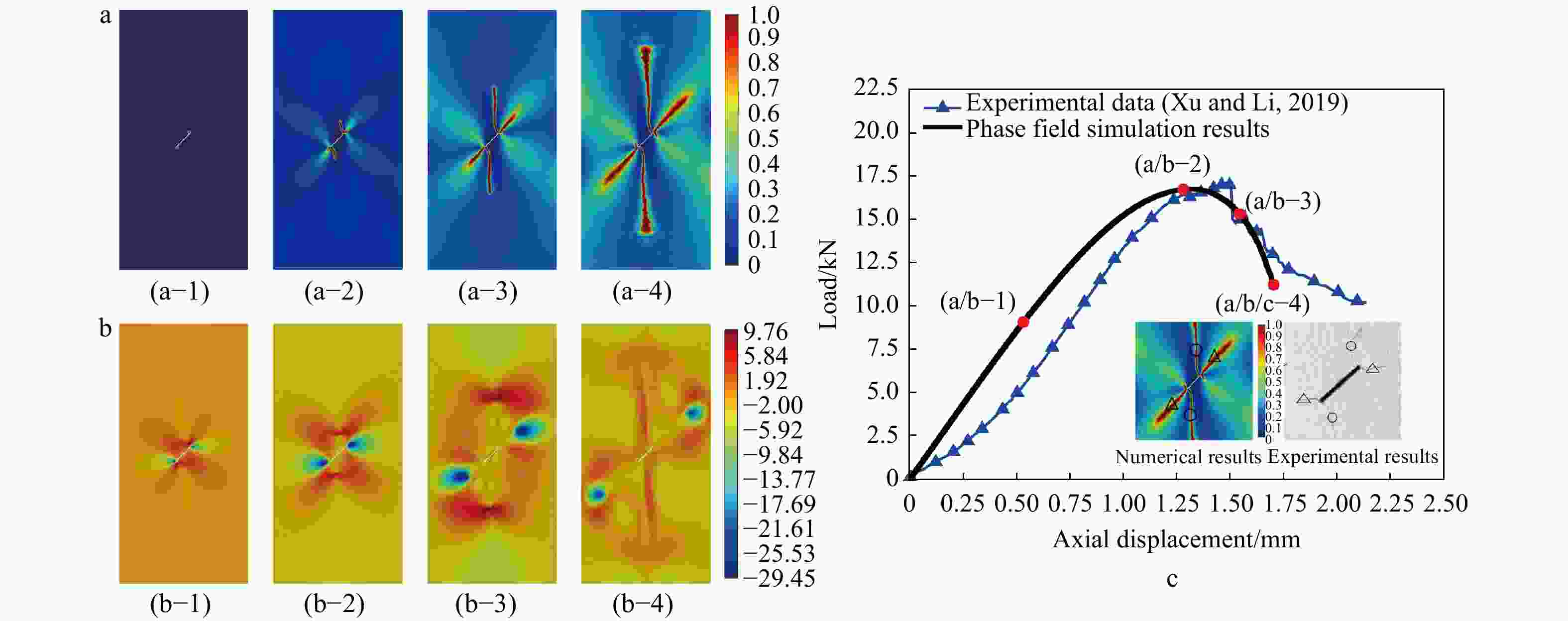
图  5  含单条裂隙的类岩试样在单轴压缩试验中的渐进破坏过程

a—裂纹扩展路径；b—最大主应力分布；c—与实验结果的对比（Xu and Li， 2019）

Figure  5.  Progressive failure process of a fissured rock-like sample consisting of a single fissure in the uniaxial compression test

(a) Crack growth paths; (b) Maximum principal stress; (c) Compression with laboratory experiments (Xu and Li, 2019)

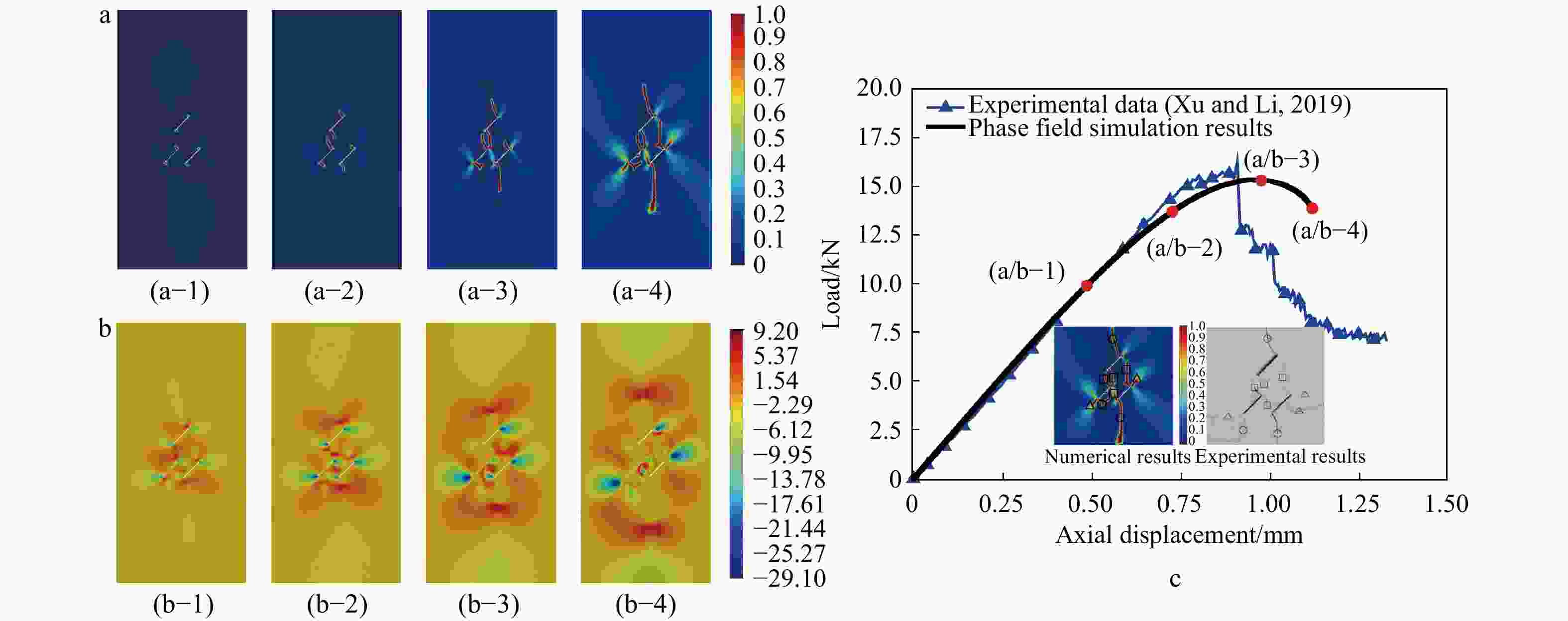
图  6  含3条裂隙的类岩试样在单轴压缩试验中的渐进破坏过程

a—裂纹扩展路径；b—最大主应力分布；c—与实验结果的对比（Xu and Li，2019）

Figure  6.  Progressive failure process of a fissured rock-like sample containing three pre-existing fissures in the uniaxial compression test

(a) Crack growth paths; (b) Maximum principal stress; (c) Compression with laboratory experiments (Xu and Li, 2019)

图  7  砂岩试样的几何形状与边界条件

a—V形缺口高孔隙砂岩试样；b—在三轴压缩试验中含有中心弱点的完整高孔隙砂岩试样的几何形状与边界条件

Figure  7.  Geometric and boundary conditions of sandstone samples

(a) V-shaped notched high-porosity sandstone sample; (b) Intact high-porosity sandstone sample containing one centered weak point in triaxial compression tests

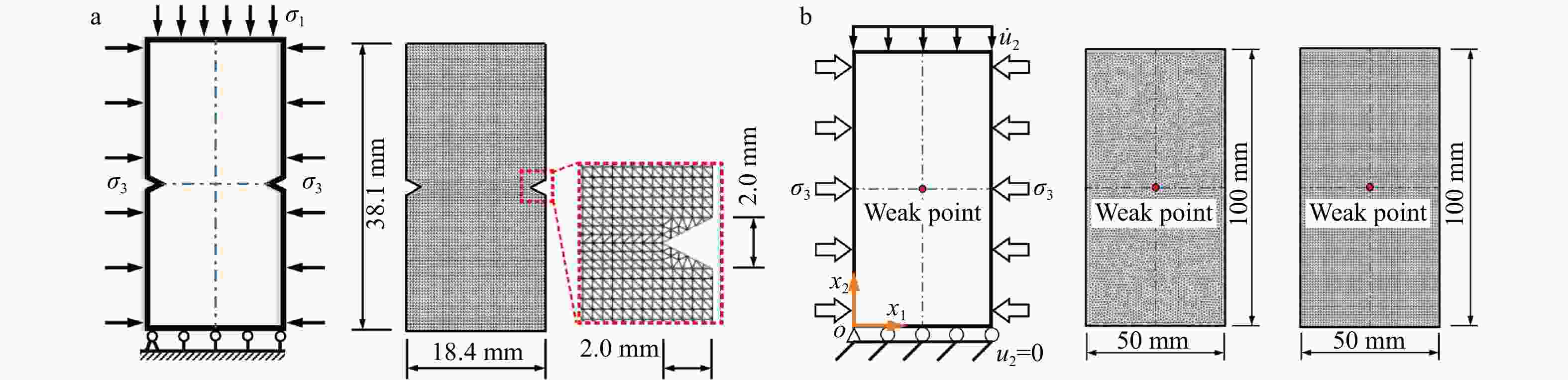
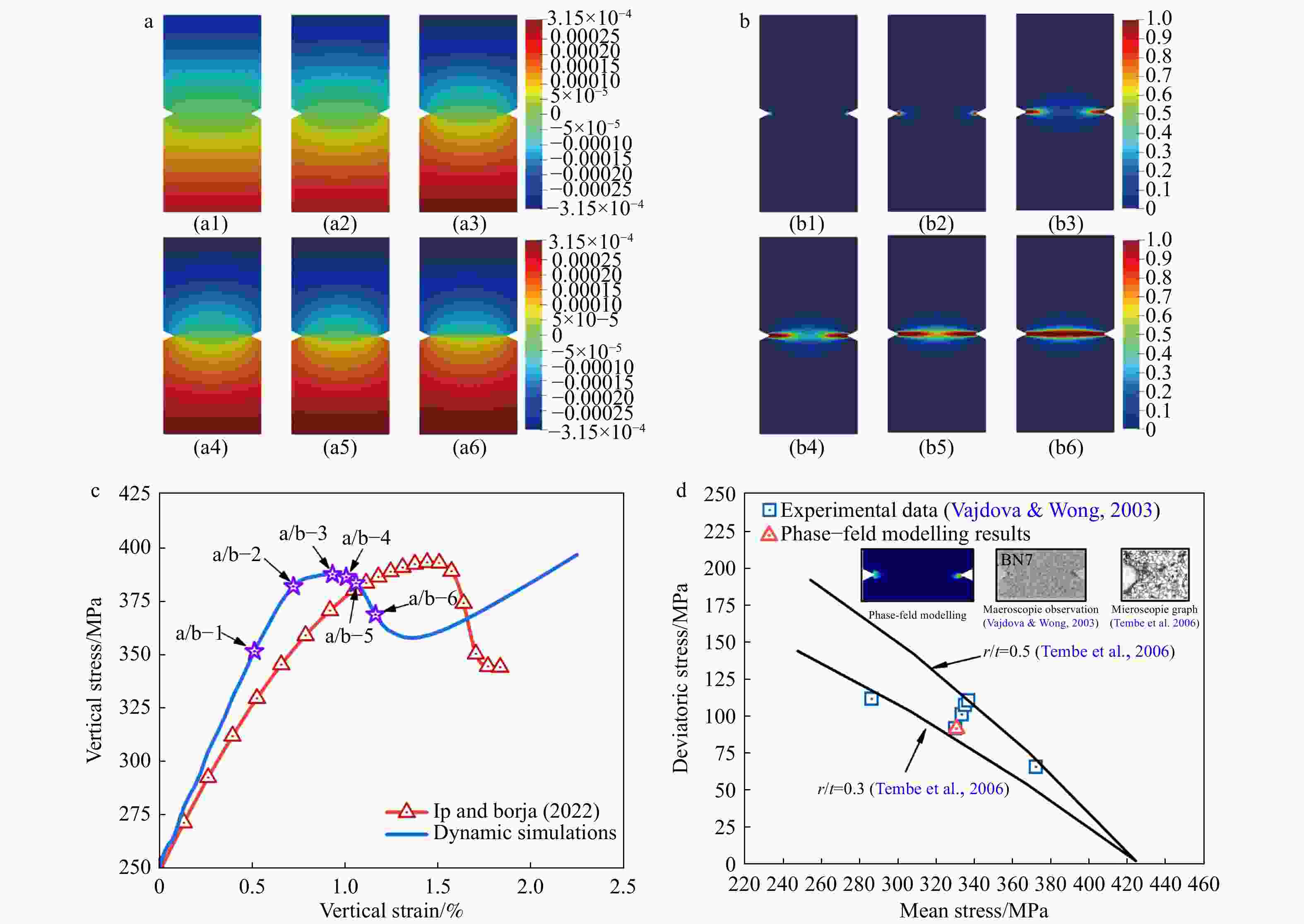
图  8  缺口砂岩试样中压实带形成的数值结果

a—竖向位移场；b—压实带形成；c—模拟应力–应变曲线与 Ip and Borja（2022）的结果对比；d—相场模拟、实验（Vajdova and Wong，2003）及 LEFM 理论分析（Tembe et al.，2006）得到的初始屈服应力

Figure  8.  Numerical results of compaction bands formation

(a) Vertical displacement field (unit: m); (b) Compaction band formation; (c) Comparison of the simulated stress–strain response with the simulation result of Ip and Borja (2022); (d) Initial yield stress for the notched Bentheim sandstone samples obtained from the phase–field simulation, laboratory tests (Vajdova and Wong, 2003) and LEFM theoretical analysis (Tembe et al., 2006)

图  9  平面应变压缩试验中侧向应力 σ₃ 对局部变形带形态的影响

Figure  9.  Effect of $ {\sigma }_{3} $ on the localized deformation band patterns in the plane strain compression tests

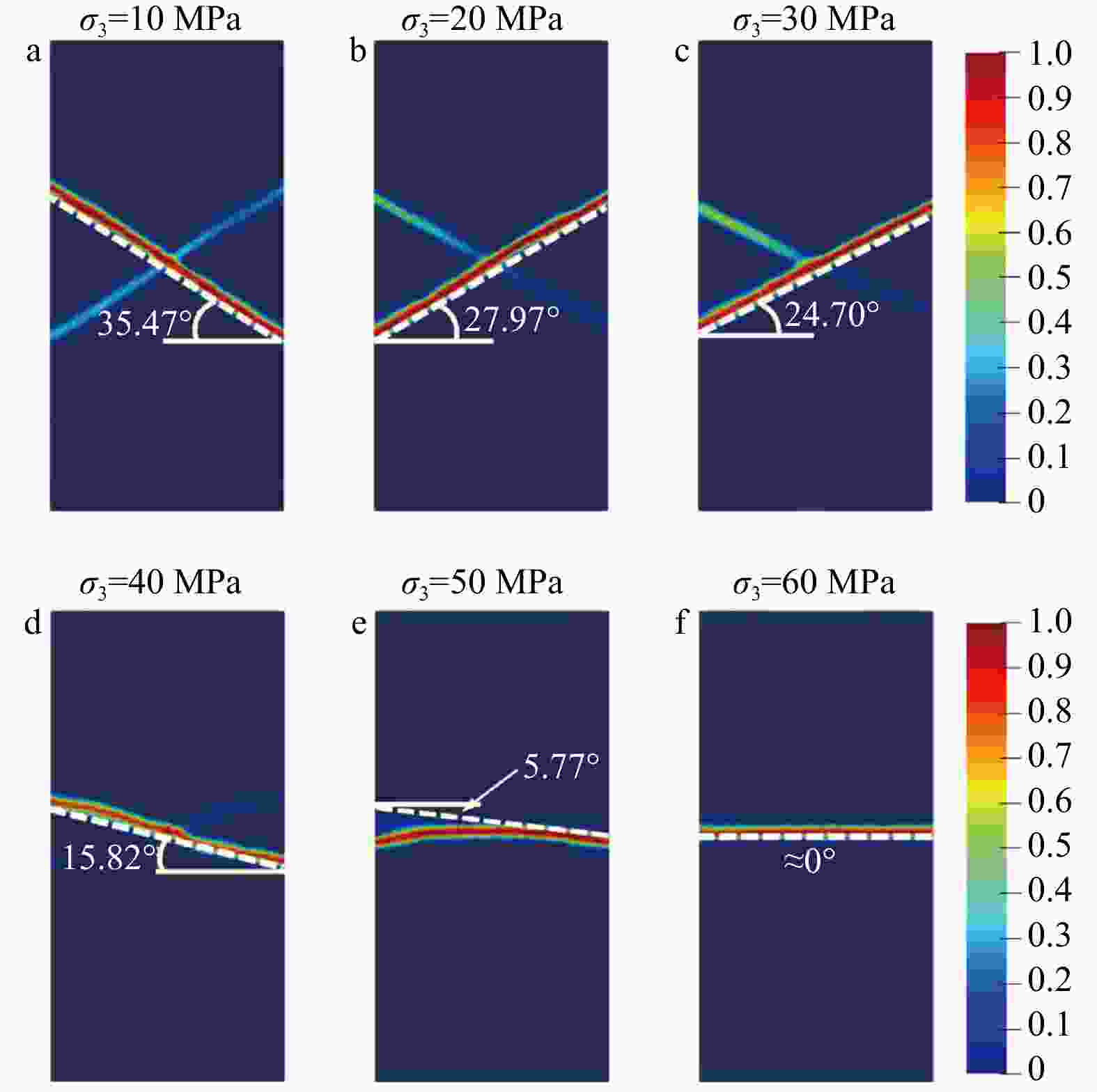
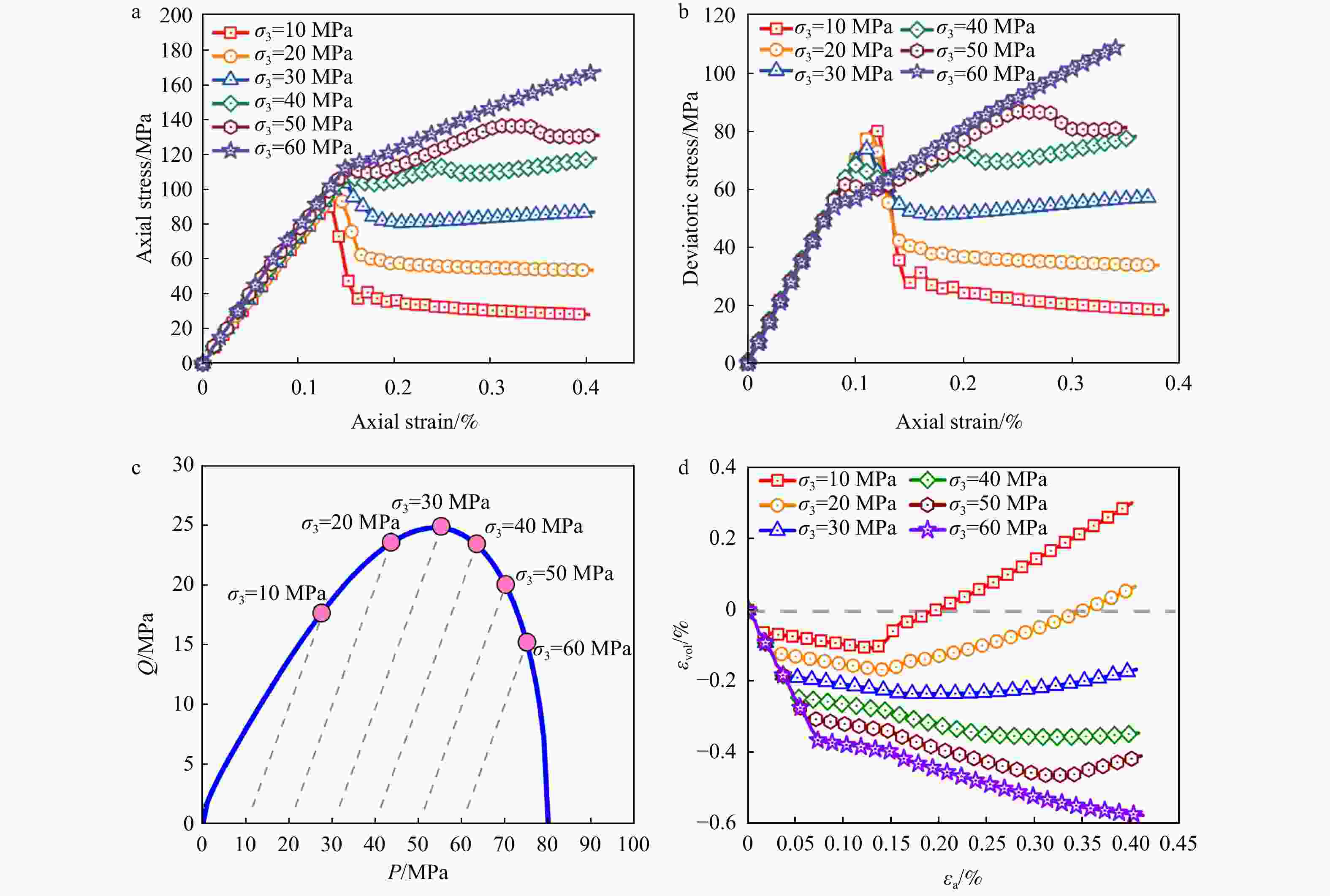
图  10  围压对力学响应的影响

a—$ \sigma_1 - \varepsilon_1 $ 曲线；b—$ \mathcal{Q}-{\varepsilon }_{1} $ 曲线；c—应力路径与初始屈服面关系；d—$ {\varepsilon }_{\mathrm{v}\mathrm{o}\mathrm{l}}{-}{\varepsilon }_{1} $曲线

Figure  10.  Effect of $ {\sigma }_{3} $ on mechanical behavior

(a) $ \sigma_1\text{–}\varepsilon_1 $ curves; (b) $ \mathcal{Q}\text{–}\varepsilon_1 $ curves; (c) Relations between loading stress paths and the initial yield surface; (d) $ \varepsilon_{\mathrm{v}\mathrm{o}\mathrm{l}}-\varepsilon_1 $ curves