0.   引言

破裂（fracture，包括断层和节理）是岩石圈最基本的构造要素之一（Twiss and Moores，1992），是脆性变形的基本方式。几乎所有的内动力地质作用和大部分外动力地质作用都与之相关，同时资源和能源的形成（特别是资源，如石油和天然气）和地质灾害的发生（如地震、滑坡等）都直接或间接地与之相关（徐开礼和朱志澄，1989；Twiss and Moores，1992）。

从物理本质上，岩石破裂形成存在两种基本方式：剪切破裂和扩张破裂（Twiss and Moores，1992）。

岩石发生剪切破裂的经典准则是Coulomb-Mohr准则（Twiss and Moores，1992）。然而，Coulomb-Mohr准则只适用于均匀介质，产生的断层是方位优选的（Anderson，1951），而且只能预测破裂发生前的瞬间趋势（不能用来分析破裂发生后的递进变形过程；Tong et al.，2010），实际应用中存在显著局限。在岩石力学实验基础上提出的、以Byerlee律（Byerlee，1978）为代表的滑动摩擦律克服了均质体的假设和斜向滑动的问题（Wallace，1951；Bott，1959；Byerlee，1978），但这些模型都局限于二维应力状态。

广义剪切活动准则（Tong et al.，2010；Tong and Yin，2011；童亨茂等，2015）从产生剪切破裂的物理本质（作用在介质潜在剪破裂面上的剪应力克服该界面上的内聚力和（内）摩擦力，即可产生剪切破裂）出发，应用“先存构造活动性准则”（Activation criterion of pre-existing fabric；Tong et al.，2010）和“活动趋势分析理论”（Theory of activation tendency analysis；Tong and Yin，2011），提出了适用于任意应力状态、任意介质的脆性剪切活动准则，从理论上建立了适用于实际地质体的剪切活动准则。但该准则只适用于判别剪切活动。

扩张破裂的经典准则是Griffith准则（Griffith，1921）。该准则考虑了微裂纹的应力集中效应，解决了宏观物体的破裂强度大大低于理论值的问题，但没有涉及具有宏观先存构造（包括具有内聚力的薄弱面和没有内聚力的先存破裂构造）的扩张破裂问题。如有天然裂缝发育的页岩，压裂过程中产生的破裂就不能简单地用Griffith准则来判别，因为压裂过程中，不仅产生垂直最小主应力方向的张裂缝，而且先存的天然裂缝也可能产生扩张活动（童亨茂等，2021a）。

经典的破裂准则（包括Coulomb-Mohr准则和Griffith准则）均没有考虑宏观先存构造，而实际地质体普遍发育宏观先存构造（薄弱面），如断层、节理、层理、软弱层、面理、不整合面、侵入接触边界等。这些先存构造有的有内聚力（如层理、面理等），有的没有内聚力或内聚力很小（如断层和节理）。在有先存构造的情况下，无论是扩张破裂还是剪切破裂均可能不是方位优先的。针对实际的地质体，经典破裂准则存在显著的局限性。

另外还存在一个没有得到很好解决的问题：当最小有效主应力为零或负值（张应力）的应力状态时，地质体如何产生脆性破坏，即在这种应力状态下，剪切活动能否产生？是否只能产生扩张破裂？这些问题在理论上一直没有得到很好的解决。

针对上述问题，文章从脆性破裂（剪切破裂和扩张破裂）的物理本质出发，结合广义剪切活动准则，提出了在任意应力状态下，用破裂趋势因子（fracturing tendency factor，f_F，无量纲）定量评价有宏观先存构造地质体中任意界面（包括薄弱面）发生破裂及进一步活动（合称破裂活动）的可能性及破裂活动的类型（扩张破裂活动或剪切破裂活动），即“广义破裂活动准则”。该准则不仅克服了经典的扩张破裂准则和剪切破裂准则存在的局限，而且把它们统一在了一起，并把破裂扩展到破裂活动，理论上适用于任何实际的地质体，应用前景广阔。

1.   破裂→破裂活动

在岩石力学实验中，岩石样品在围压不太高的情况下一旦发生宏观破裂就会失去承载力，实验一般到此结束，因此很少再去关心岩石发生破裂以后的事情，包括已有的破裂准则。然而，地质体则不同，发生破裂后，承载力虽然会有一定不同程度的减小（如地震后发震断层附近产生应力降（Bailey and Ben-Zion，2009），但不会完全失去。破裂产生以后，只要载荷（如构造作用力、工程注入流体压力等）继续存在，破裂作用就会继续。其中，剪切破裂发生后，还会沿破裂面产生剪切滑移（断层作用）；张破裂发生后，破裂面还会产生扩张（扩张作用）；同时，破裂活动过程中，破裂面均会不同程度地产生扩展（破裂面变大）。

地质体产生破裂及其后续的活动，文中统称为破裂活动（fracturing activity），并划分为剪切破裂活动（简称剪切活动）和扩张破裂活动（简称扩张活动）。

在有先存薄弱面（带）的情况下（尤其是含有没有黏聚力的先存破裂），破裂活动与均质体存在很大的区别。在载荷作用下，没有黏聚力的先存破裂的破裂活动直接进入破裂的后续活动阶段（扩张或滑移），破裂面的扩展方式也比较独特（Tong et al.，2014）。经典的Coulomb-Mohr准则和Griffith准则均没有考虑宏观先存构造，不适用于有先存薄弱面地质体，也无法解释和预测其破裂作用过程。

需要特别指出的是，简单地用“破裂”一词难以准确地描述有先存薄弱面地质体的破裂作用过程，为此，文中采用“破裂活动”一词。

2.   剪切活动准则

2.1   Coulomb-Mohr准则

Coulomb剪破裂准则是Coulomb于1776年提出的（Célérier，2008），可以用公式（1）表示（徐开礼和朱志澄，1989；Twiss and Moores，1992）：

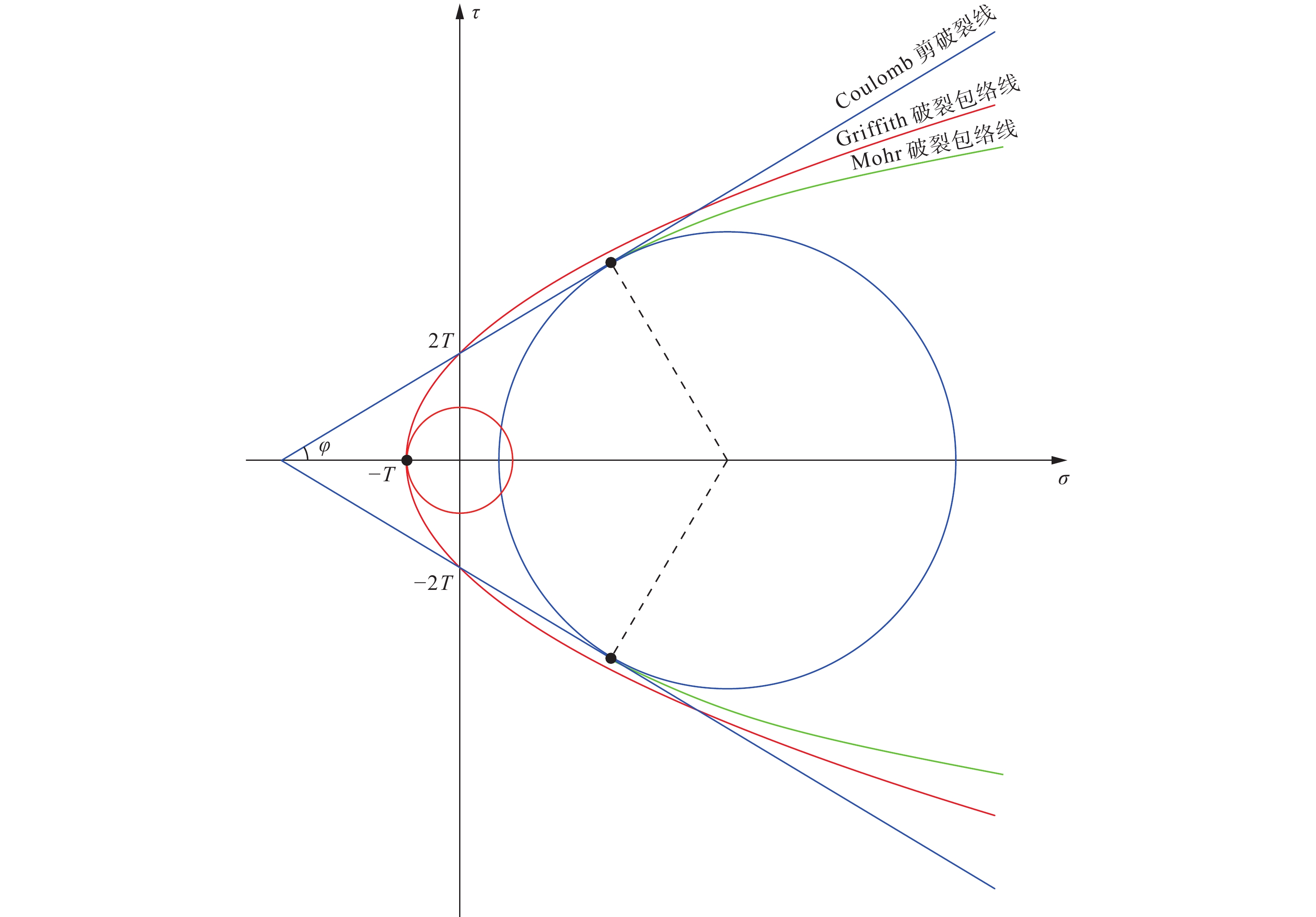
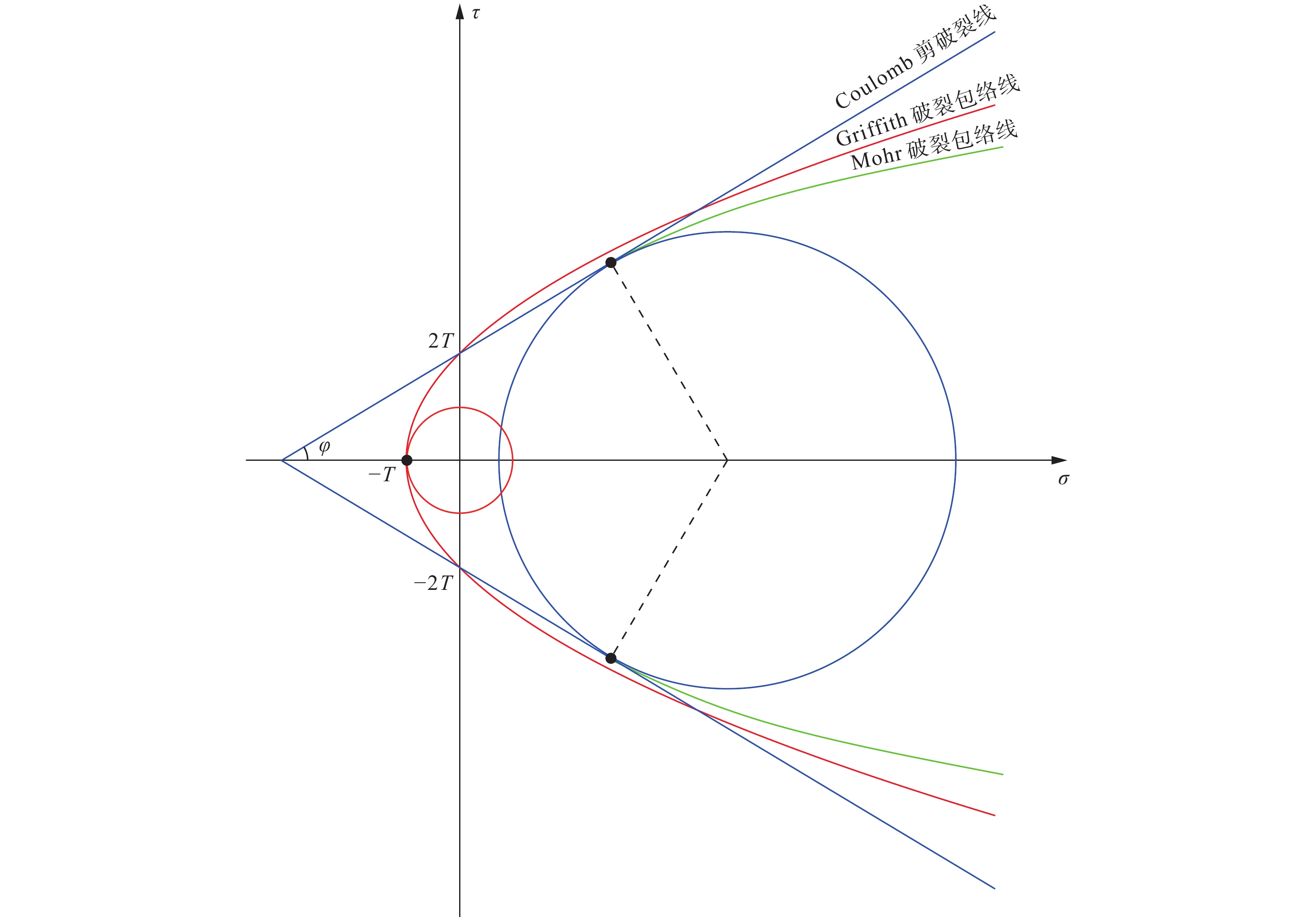
其中，τ为临界剪应力，σ_n为该截面上的正应力，C为介质的内聚力（常数），μ为介质的内摩擦系数（常数）。公式（1）在τ-σ坐标系中为一条直线（图1），称为“库伦剪破裂线”，μ为该直线的斜率。其中μ = tanφ，φ为岩石的内摩擦角，T为岩石的抗张强度，内聚力C=2T。发生Coulomb剪破裂的临界应力状态被称为Coulomb应力状态。文中的应力符号采用固体力学的定义（压应力为正，张应力为负）。

图  1  Coulomb-Mohr准则与Griffith准则图解

φ为岩石的内摩擦角；T为岩石的抗张强度；内聚力C=2T

Figure  1.  Diagram of Coulomb-Mohr criterion and Griffith criterion

φ is the internal friction angle of the rock, T is the tensile strength of the rock and the cohesion C=2T

下载: 全尺寸图片 幻灯片

Mohr在岩石力学实验的基础上，发现岩石内摩擦系数μ（或内摩擦角φ）并不是一个常数，它与σ_n相关，一般随着σ_n的增大而减小。这样，Mohr对Coulomb准则进行了修正（把剪破裂线从Coulomb准则的直线变为曲线即“Mohr破裂包络线”；图1），即Mohr准则。这两个经典剪破裂准则合称为Coulomb-Mohr准则。

Coulomb准则是针对均匀介质提出的（Anderson，1951）。Anderson根据Coulomb剪破裂准则，指出均匀介质的岩石在应力作用下发生的剪破裂是方位优选的，即剪破裂面与最大主压应力轴σ₁的夹角（剪裂角）等于±(45°−φ/2)（φ为内摩擦角），并与中间主应力轴σ₂平行，是一对共轭的破裂面（Anderson，1951），并进一步提出了Anderson断层模式，成为构造地质学的世纪经典理论（Célérier，2008）。但该断层模式是基于均匀介质的，在实际应用中具有显著的局限性（Tong et al.，2010）。

2.2   滑动摩擦律（Byerlee律）

基于Coulomb-Mohr准则的Anderson断层模式假定地质体是均匀介质，预测断层是方位优选的，只与主应力的方位有关，与其他因素（如先存构造面）无关。

然而，实际地质体是非均质的。先存构造（主要是先存断裂）对非均质性的影响一般最为显著，是造成地质体非均质的主导因素（童亨茂等，2009；Tong et al.，2010），这是造成Anderson模式存在局限、无法很好地解释自然界断层作用现象的根本原因。

为了解决在先存构造面上断层复活的问题，不同学者先后提出了摩擦滑动律（Wallace，1951；Bott，1959；McKenzie，1969；Byerlee，1978；Jaeger and Cook，1979）和滑动趋势分析理论（Morris et al.，1996）。

摩擦律认为，先存破裂在地应力作用下，当作用在先存破裂面上的剪应力克服其内聚力和摩擦力后，先存破裂可以重新活动（Bott，1959；McKenzie，1969；Byerlee，1978），其中最著名的是在实验基础上提出的Byerlee律（Byerlee，1978），可以用公式（2）表示。

式中，τ_W为临界剪应力，C_W为先存破裂面的内聚力，σ_n为先存破裂面上的正应力，μ_W为先存破裂面上的摩擦系数。

摩擦滑动律提出沿先存构造面滑动的断层作用克服了Anderson断层模式中均质体的假设和斜向滑动的问题（Wallace，1951；Bott，1959；Byerlee，1978），但这些模型都局限于二维应力分析（Morris et al.，1996）。滑动趋势分析理论把沿薄弱面的摩擦滑动分析从二维扩展到三维，但该模型也具有一定的局限性：一是只考虑Anderson应力状态（一个主应力轴直立）；二是忽略了薄弱面的内聚力；三是没有考虑岩石内摩擦系数的变化（Tong and Yin，2011）。

滑动摩擦律在一定程度上克服了Anderson模式的局限性，但都没有从根本上解决自然界复杂介质条件下断层作用的力学机制问题。

2.3   广义剪切活动准则

分析Coulomb-Mohr准则和Byerlee律可以看出，不论是均匀介质还是非均匀介质，产生剪切活动的物理本质是共同的，即作用在界面上的剪应力只要能克服该界面上的内聚力和（内）摩擦力，即可产生剪切活动。

文中使用“剪切活动”而非“剪切破裂”一词，是因为沿失去内聚力（已经破坏）的先存构造面发生剪切活动不需要再发生剪切破坏，即“剪切活动”存在两种情况：一是产生剪切活动的潜在界面是有内聚力的，则剪切活动通过剪切破坏而产生，需要克服内聚力和（内）摩擦力；二是产生剪切活动的界面无内聚力，则剪切活动只需克服界面的摩擦力即可产生。

童亨茂等（2015）提出的广义剪切活动准则从剪切活动的物理本质出发，应用先存构造面活动准则和活动趋势分析理论，提出用剪切活动趋势因子（f_S；公式（3））来表达任意三轴应力状态下，任意界面（方位定义见图2）发生剪切活动的可能性（具体公式推导过程见Tong et al.，2010）：

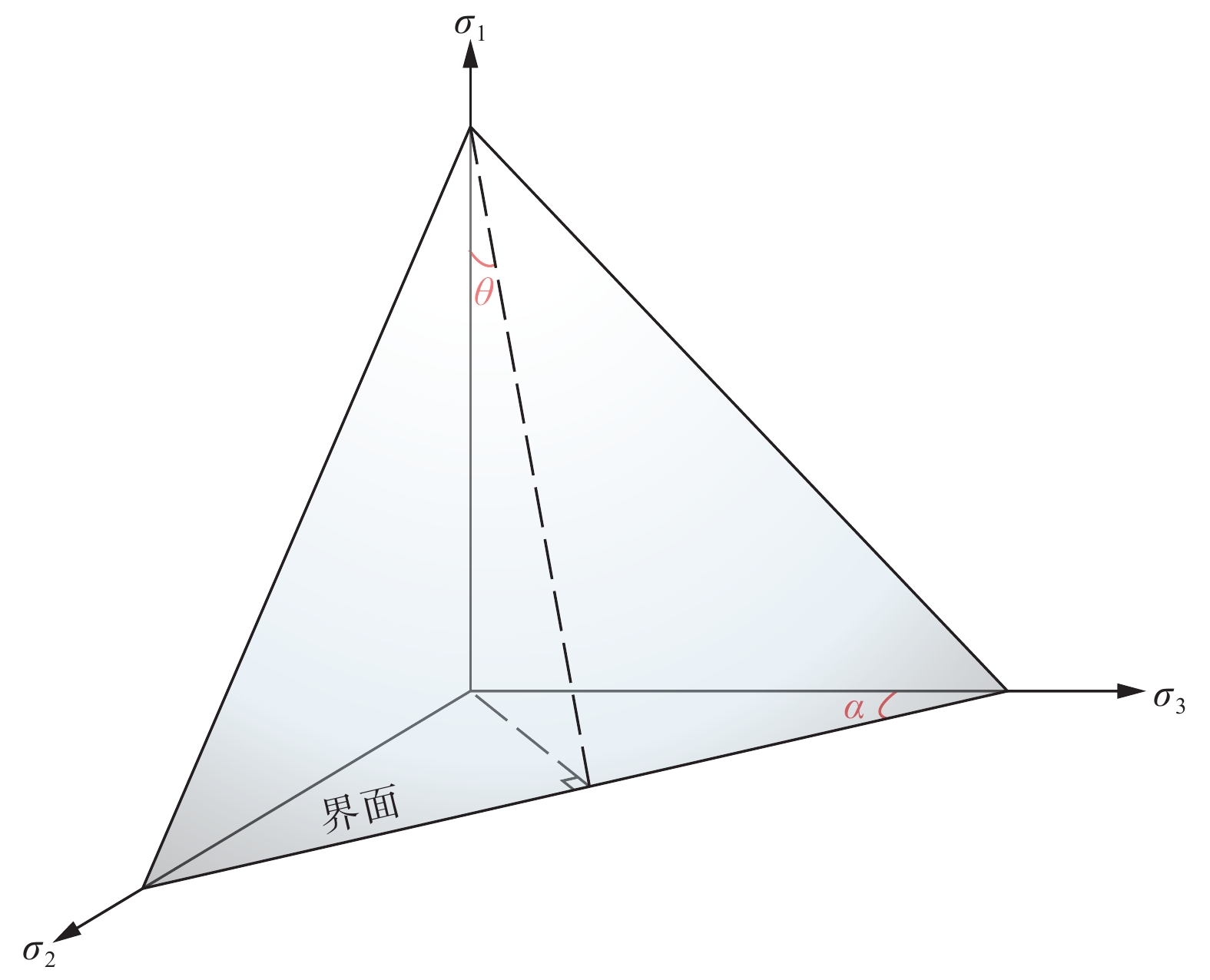
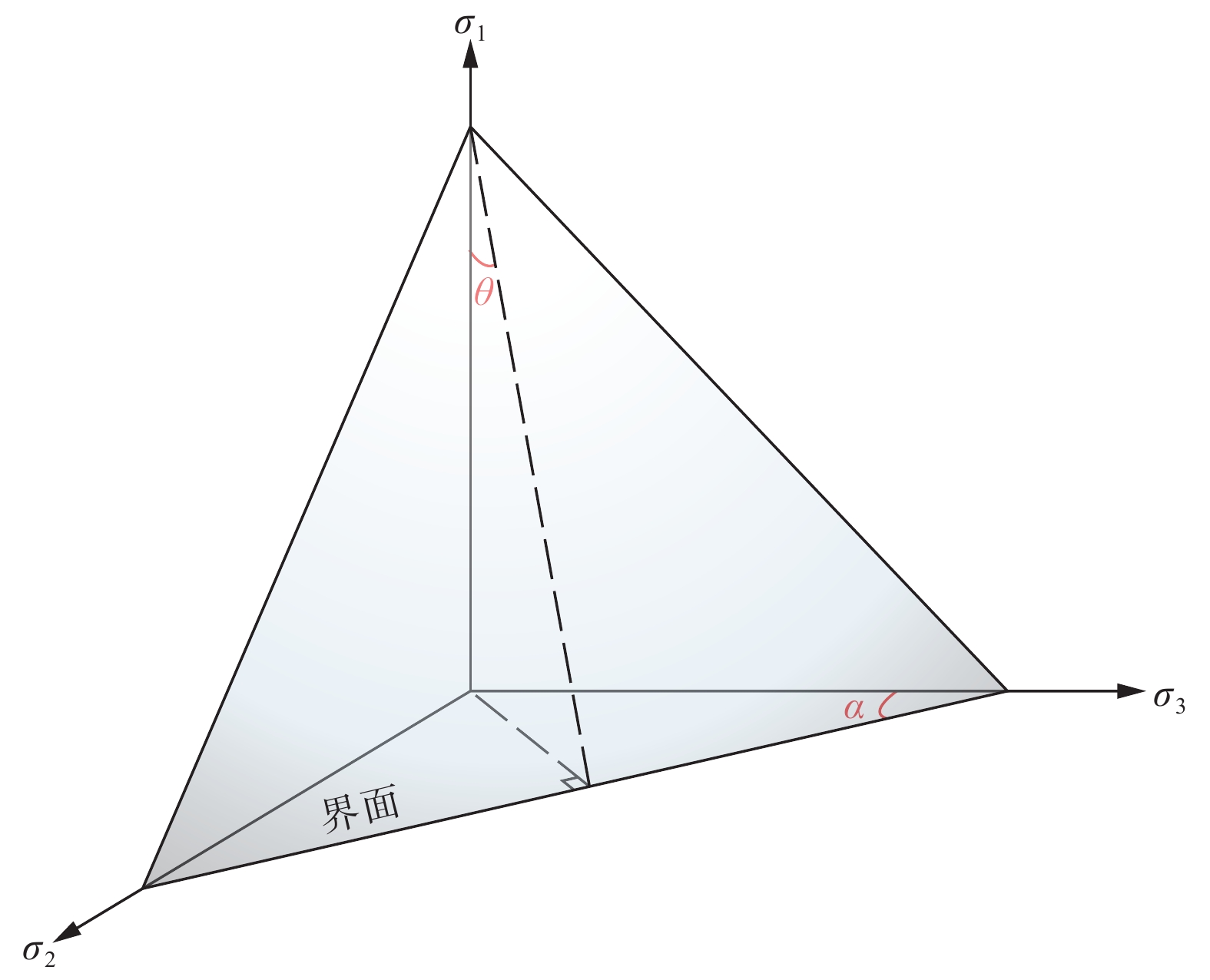
图  2  界面的空间方位定义（以3个主应力为坐标轴）

σ₁、σ₂和σ₃分别为最大、中间和最小主应力；θ为界面与σ₁的夹角；α为界面在σ₂−σ₃平面上的交线与σ₃的夹角

Figure  2.  The spatial orientation definition of the interface (with 3 principal stresses as axes)

σ₁, σ₂ and σ₃ are the maximum, intermediate and minimum principal stresses respectively, θ is the angle between the interface and σ₁, and α is the angle between σ3 and the interface's intersection line with the σ₂–σ₃ plane.

下载: 全尺寸图片 幻灯片

式中，σ₁，σ₂和σ₃分别为最大、中间和最小主应力；C_P为界面的内聚力；μ_P为界面上的摩擦系数；θ为界面与σ₁的夹角；α为界面在σ₂−σ₃平面上的交线与σ₃的夹角。需要说明的是，界面的地理方位（如倾向和倾角）与θ和α之间的关系可以通过坐标转换来建立（Tong and Yin，2011）。

很容易验证，当C_P = C，μ_P = μ，即在均匀介质的情况下，若f_S= 1.0（即发生临界剪切活动），公式（3）可以简化成公式（1），即Coulomb-Mohr准则。这样，Coulomb-Mohr准则是公式（3）在均匀介质和临界剪切活动情况下的端元。同样很容易验证，滑动摩擦律的代表Byerlee律是公式（3）在二维应力状态下（界面与中间主应力σ₂轴平行），界面处于临界剪切活动状态（f_S = 1.0）的端元（童亨茂等，2015）。这样，公式（3）就把Coulomb-Mohr准则和以Byerlee律为代表的滑动摩擦律统一在了一起。

此外，应用有限单元的思想，只要进行有限单元的划分，任何类型的实际非均匀地质体，都可以看作是平面（板）状先存构造（薄弱带）和均匀介质的组合体（如含一条平面状断层的均匀地质体；童亨茂等，2015）。因此，从理论上，公式（3）适用于任何实际的地质体。

剪切活动趋势因子f_S（公式（3））一方面把经典的剪切破裂准则Coulomb-Mohr准则和Byerlee律统一起来，并把它们作为其中的端元；另一方面，理论上适用于任何非均匀介质和任意应力状态。为此，将公式（3）称为“广义剪切活动准则”，可以定量判断任意介质、在任意三轴应力状态下、任意方位界面（包括先存薄弱面和非薄弱面）发生剪切活动的可能性（童亨茂等，2015）。广义剪切活动准则用无量纲的剪切活动趋势因子定量描述地质体中不同先存构造面发生剪切活动的可能性及活动能力大小，从理论上解决了实际地质体断层作用的力学机制问题，为实际地质体断层作用模型的建立提供了理论基础。

3.   张破裂准则

经典的张破裂准则是Griffith准则。Griffith（1921）指出，产生破裂与微裂纹的存在有关，当σ₃ = −T、σ₁<−3σ₃时，微裂纹产生扩展并最终形成与σ₁平行的张破裂；当(σ₁−σ₃)²/(σ₁+σ₃) ≤8T时（假定材料的抗压强度是抗张强度的8倍），则与σ₁大约呈30°角的微裂纹最易扩展并产生破裂，破裂包络线方程为：

式中，τ_n为临界剪应力，T为岩石的抗张强度，σ_n为该截面上的正应力。

Griffith准则考虑了微裂纹的应力集中效应，解决了宏观物体的破裂强度大大低于理论值的问题；同时该准则实质上把张破裂和剪切破裂联合起来了（图1显示公式（4）在应力摩尔圆图解上是一条抛物线型的破裂包络线）。但Griffith准则没有涉及具有宏观先存构造（包括没有内聚力的破裂面和具有内聚力的先存薄弱面）的扩张破裂问题，也没有阐述抛物线型的破裂包络线不同段落所代表的物理本质。

4.   广义破裂活动准则

4.1   破裂活动的物理本质

剪切活动和扩张活动的力学机制存在差异，下面分别加以分析。

不论是均匀介质还是非均匀介质，产生剪切活动的物理本质是共同的，即只要作用在任意界面（先存薄弱面或假想界面）上的剪应力能克服其内聚力和（内）摩擦力，该界面即可产生剪切活动（童亨茂等，2015）；同样，产生扩张活动的物理本质也是共同的，即只要作用在任意界面（先存薄弱面或假想界面）上的有效正应力（σ_n−P₀）能克服其扩张强度T_P（指界面两侧介质间的黏聚力，对于非薄弱面，T_P = T，P₀为界面上的流体压力），该界面即可产生扩张活动，即当σ_n−P₀ = −T_P时，界面即可产生扩张活动。在地壳应力状态下，3个主应力一般都是挤压应力，出现张应力的情况可以忽略（Zoback，2007），地质体内产生扩张活动一般必须有流体压力参与才能实现。因此，一般情况下，地质体内界面产生扩张破裂的物理实质是：流体压力克服了界面上的正应力和扩张强度。

4.2   广义扩张活动准则

广义剪切活动准则用无量纲的剪切活动趋势因子（f_S；公式（3））定量描述地质体中不同构造面（先存薄弱面或假想界面）发生剪切活动的可能性及活动能力大小。按照类似的思想，文中定义扩张活动趋势因子（f_T；公式（5））来定量描述地质体中不同界面（先存薄弱面或假想界面，界面的方位也按图2定义）发生扩张活动的可能性及活动能力大小：

按照界面方位在图2中的定义，可以推导出任意三轴应力状态下、任意方位界面f_T的表达式（公式6）：

在给定的应力状态下，当f_T = 1.0，界面处于临界扩张活动状态；f_T> 1.0，界面已发生扩张活动；f_T< 1.0，界面处于稳定状态。

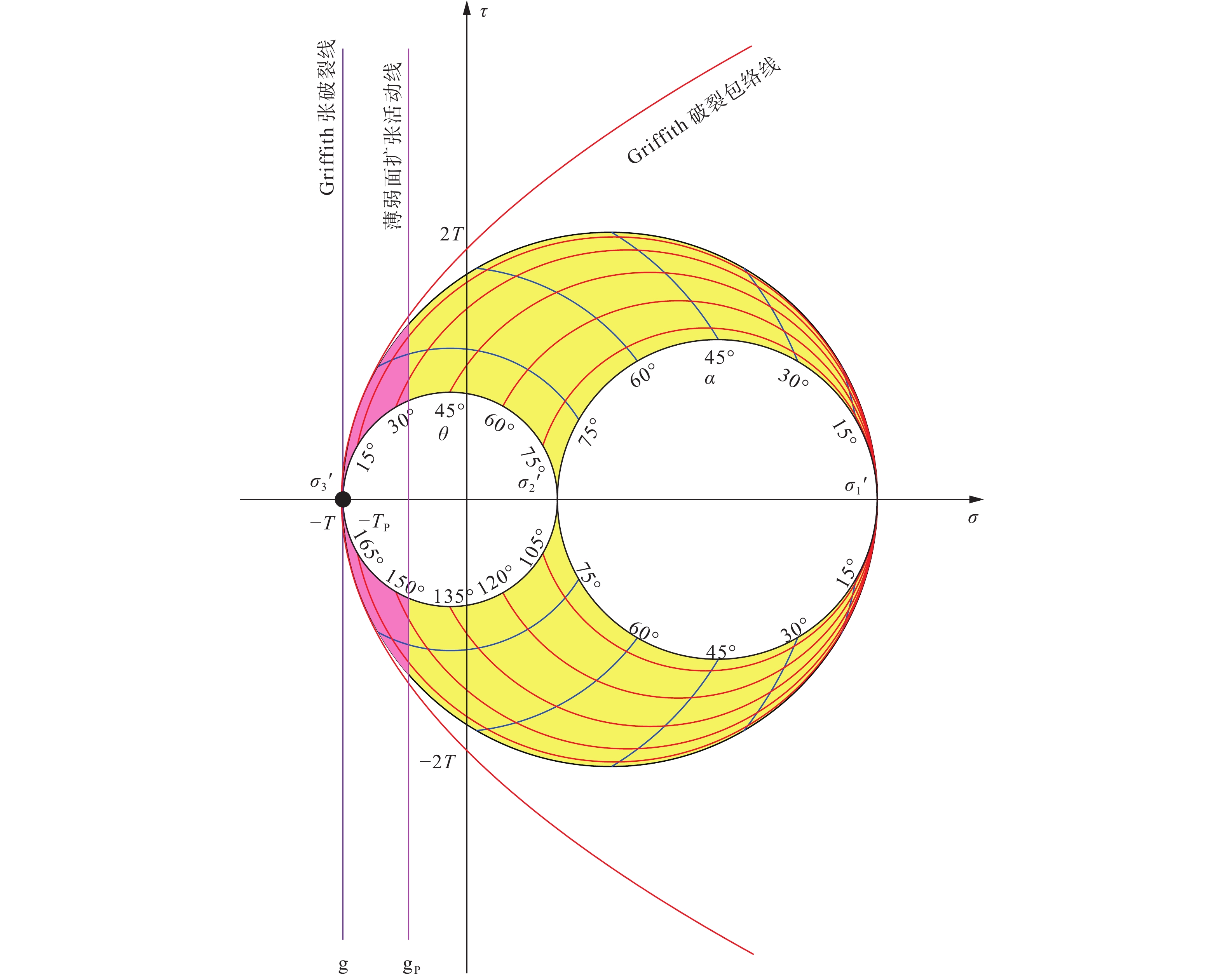
利用摩尔空间（图3）很容易验证，当f_T = 1.0、T_P = T（即均匀介质）时，只有与σ₃垂直的界面（θ= 0°、α =90°）才能满足扩张破裂的条件（其它方位的界面均无法满足），把f_T = 1.0、T_P = T、θ= 0°、α =90°代入到公式（6），即可得到：σ₃′ = −T（其中σ₃′ = σ₃−P₀，表示最小有效主应力），这表明：①经典的Griffith张破裂准则是公式（6）为均匀介质（T_P = T）处于临界扩张活动条件（f_T = 1.0）时的端元；②均匀介质产生的扩张破裂是方位优选的，即扩张破裂面垂直于σ₃。文中把σ₃′ = −T的应力状态称为Griffith应力状态，与横坐标轴垂直且截距为−T的直线称为Griffith张破裂线（图3中直线g），同时把与横坐标轴垂直且截距为−T_P的直线称为薄弱面扩张活动线（图3中直线g_P）。

图  3  Griffith应力状态下的摩尔空间图解

T为岩石的抗张强度；2T为岩石的内聚力；T_P为薄弱面的扩张强度；g为Griffith张破裂线；g_P为薄弱面的扩张活动线；θ 为界面与 σ ₁的夹角； α 为界面在 σ ₂− σ ₃平面上的交线与 σ ₃的夹角

Figure  3.  Diagram of the Mohr space under Griffith stress state

T is the tensile strength of the rock, 2T is the cohesion of the rock, T_P is the extension strength of the weakness plane, g is the Griffith tensile fracture line, g_P is the extension activation line of the weakness plane, θ is the angle between the interface and σ ₁, and α is the angle between σ ₃ and the interface's intersection line with the σ ₂- σ ₃ plane.

下载: 全尺寸图片 幻灯片

而在有薄弱面存在的情况下（T_P<T），当达到Griffith应力状态时，位于图3粉色区域（直线g_P左侧（含）的摩尔空间区域）不同方位的薄弱面均已达到了扩张破裂的条件（f_T ≥ 1.0）。这表明在有薄弱面存在的情况下，产生的扩张破裂不是方位优选的。

考虑到公式（6）适用于任意有薄弱面的非均匀介质（包括任何实际的地质体）以及任意方位的界面，且涵盖了经典的张破裂准则，将其称之为广义扩张活动准则。

4.3   广义破裂活动准则

由于剪切活动趋势因子（f_S）和扩张活动趋势因子（f_T）均是无量纲的，数值可直接对比。在给定的应力状态下，通过对比任意给定界面f_S和f_T值的大小，即可判定其是否发生破裂活动及破裂活动的类型。当f_S>f_T ≥ 1.0或f_S ≥ 1.0 >f_T时，界面发生剪切活动；当f_T>f_S ≥ 1.0或f_T ≥ 1.0>f_S时，界面发生扩张活动；当f_S = f_T ≥ 1.0时，界面发生扩张活动和剪切活动的可能性一致；当f_T< 1.0且f_S< 1.0时，界面保持稳定。为此，文中把公式（3）和公式（6）合称为广义破裂活动准则，并用公式（7）表达：

式中，f_F为破裂活动趋势因子。

考虑到除先存薄弱面外，介质发生破裂均是方位优选的。因此，广义破裂活动准则中的“界面”实际针对的是各种薄弱面和方位优选的界面。

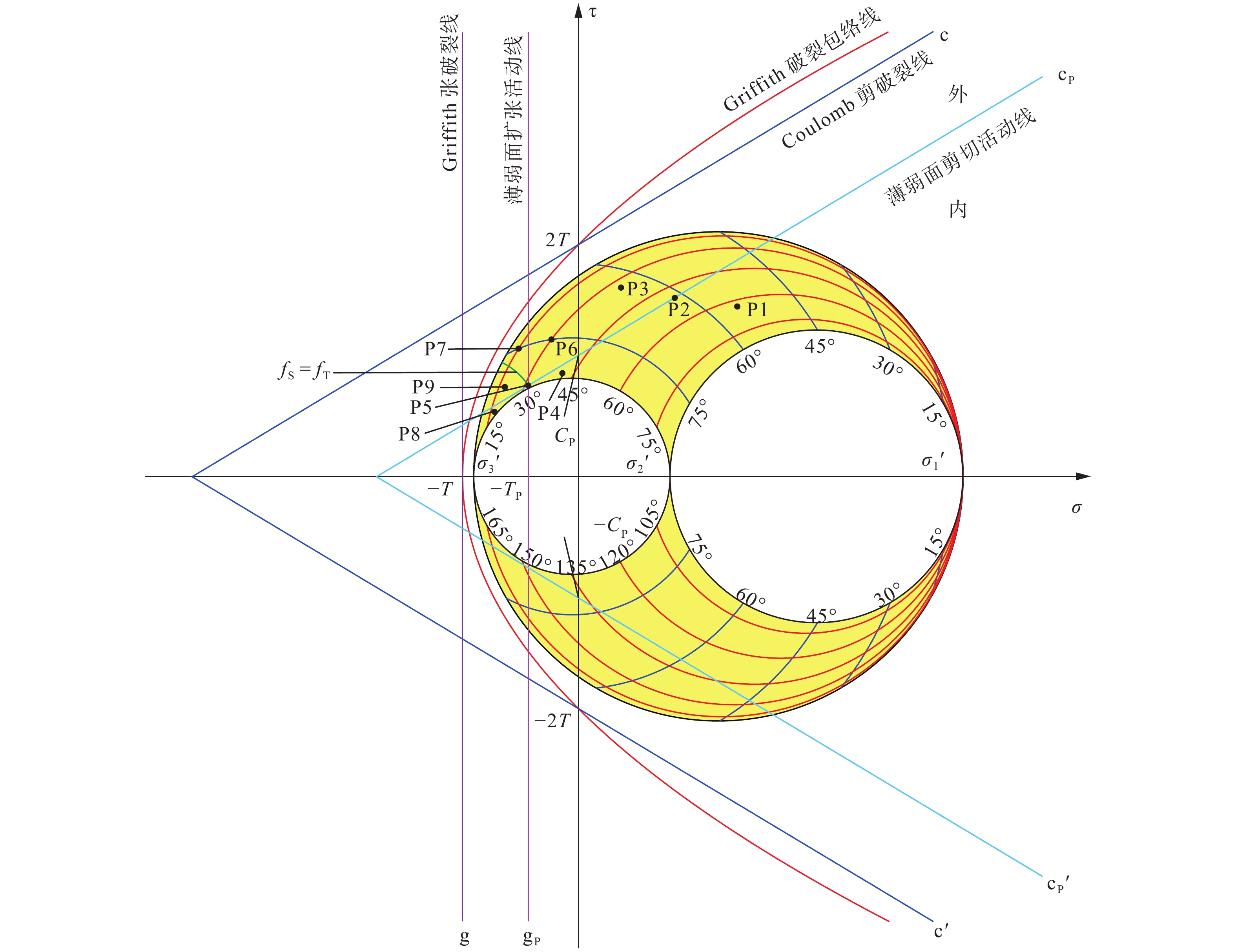
需要特别注意的是，由于Coulomb应力状态和Griffith应力状态均是介质承受应力的极限，介质的应力状态不可能超越Coulomb应力状态和Griffith应力状态，即其在摩尔空间中的极点（投影点）不可能越过Coulomb剪破裂线（图4中的直线c和c′）及Griffith张破裂线（图4中的直线g）。这是个简单而特别重要的认识。

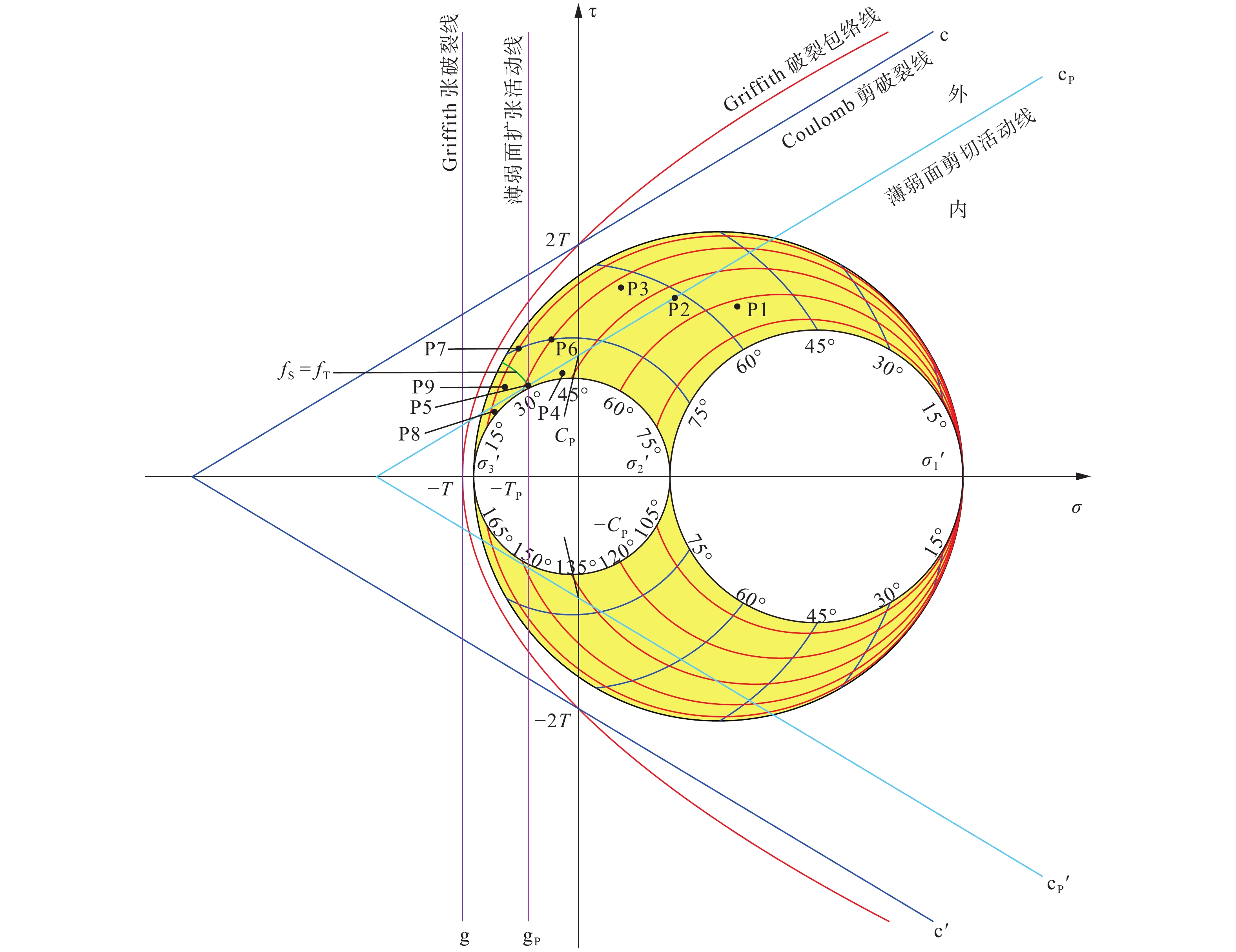
图  4  给定应力状态下摩尔空间中不同极点与破裂活动线的关系图解

T为岩石的抗张强度；2T为岩石的内聚力；C 为介质的内聚力；C _P为界面的内聚力T_P为薄弱面的扩张强度；g为Griffith张破裂线；g_P为薄弱面的扩张活动线；P1—P9为不同薄弱面在摩尔空间中的极点位置

Figure  4.  Diagram of relationship between different poles and fracturing activity line in Mohr space under given stress state

T is the tensile strength of the rock, 2T is the cohesion of the rock, C is the cohesion of the medium, C_P is the cohesion of the interface, T_P is the extension strength of the weakness plane, g is the Griffith tensile fracture line, g_P is the extension activation line of the weakness plane, and P1–P9 are the pole positions of different weakness planes in Mohr-space.

下载: 全尺寸图片 幻灯片

利用摩尔空间（图4）可以非常直观地表达广义破裂活动准则。① 摩尔空间中界面的极点位于纵坐标轴的右侧时（如P1、P2、P3），不会产生扩张活动，只可能产生剪切活动；当极点在其剪切活动线（图4中的直线c_P和c_P′）外侧时（如P1），该界面发生剪切活动；当极点在其剪切活动线上时（如P2），该界面处于临界剪切活动状态；当极点在其剪切活动线内侧时（如P3），该界面处于稳定状态。② 摩尔空间中界面的极点位于的纵坐标的左侧时（如P4—P9），极点在其剪切活动线内侧、同时在扩张活动线（图4中的直线g_P）右侧时（如P4），既不发生扩张活动，也不发生剪切活动；极点在其剪切活动线（含）外侧、同时在扩张活动线（含）左侧时（如P5—P9），活动类型要通过式7的计算（即比较f_S和f_T的相对大小）来确定：对于极点P5，f_S = f_T=1.0，该界面发生扩张活动和剪切活动的可能性相同；对于极点P6，f_S> 1.0 >f_T，该界面发生剪切活动；对于极点P7，f_S>f_T> 1.0，该界面也发生剪切活动；对于极点P8，f_T> 1.0 >f_S，该界面发生扩张活动；对于极点P9，f_T>f_S> 1.0，该界面也发生扩张活动。为方便表述，这里简单认为极点P5—P9的内聚力C_P和扩张强度T_P相等，它们的剪切活动线和扩张活动线重合。

5.   广义破裂活动准则的应用前景

广义破裂活动准则从破裂的物理本质出发，在给定应力状态下可以定量分析任意界面（先存薄弱面及假想界面）破裂活动的可能性及破裂活动的类型，理论适用于任何实际的地质体，并把经典的破裂准则统一在了一起。考虑到破裂活动与人类生活和生产密切相关，该准则具有广阔的应用前景。下面就此作一些简单的阐述。

5.1   揭示经典破裂准则所预测破裂方式的物理本质及存在问题

经典破裂准则包括Coulomb-Mohr剪破裂准则和Griffith破裂准则。

Anderson应用Coulomb准则指出均匀介质发生剪破裂是方位优选的，且为一对共轭剪切破裂面，但没有阐述其原因。

应用广义破裂活动准则和摩尔空间（童亨茂等，2014），可以很直观地解释均匀介质发生剪破裂是共轭的，而且是方位优选的：均匀介质在载荷作用下，当应力状态达到Coulomb应力状态时，摩尔空间与Coulomb-Mohr剪破裂线相切（上下有两个切点；图1）。此时，只有这两个切点所代表的界面达到了剪切活动的条件（f_S = 1.0），而其它方位界面均未达到剪切活动的条件（极点均位于破裂线内侧，f_S< 1.0），而且这两个界面同时达到破裂条件、剪切方向相反，两界面与最大主应力的夹角为±(45°−φ/2)，与中间主应力轴平行（两切点位于σ₁−σ₃摩尔大圆上），以共轭形式存在。

Griffith破裂准则实际上分两部分，分别为张破裂准则和剪破裂准则（公式（4））。

应用广义破裂活动准则和摩尔空间，可以很直观地解释均匀介质发生张破裂是方位优选的，即垂直于最小主应力轴方向：均匀介质在载荷作用下，当应力状态达到Griffith应力状态时，摩尔空间与扩张破裂线相切（只有一个切点，见图3）。此时，只有这一个切点所代表的界面达到了扩张活动的条件（f_T = 1.0），而其他方位界面均未达到扩张活动的条件（极点均位于破裂线右侧，f_T< 1.0），且此界面与最小主应力轴垂直。

当破裂点位于纵坐标轴（含）右侧时，Griffith准则和Coulomb-Mohr准则的破裂包络线形态是类似的（图1），但当破裂点位于纵坐标轴左侧时则差异很大。

如图1所示，Griffith破裂包络线是一条以横坐标轴为对称轴的抛物线（Coulomb剪破裂线则是直线），与横坐标轴的交点为（−T，0），与纵坐标轴的交点（即截距）为（0，±2T）。从纵坐标轴向左，Griffith破裂包络线的斜率（即内摩擦系数）不断增加，并在点（−T，0）时达到无穷大，而实际岩石的内摩擦系数一般都小于1.0，因此，Griffith破裂包络线斜率大于1的段落没有实际的物理意义。另外，按照Griffith准则，岩石的内摩擦系数仅与正应力的变化有关，与岩性无关，这显然也存在问题。

按照Griffith准则，C = 2T，这一结果同时也得到岩石力学实验结果的支持（Jaeger and Cook，1979）；岩石的摩擦系数一般为0.5～0.8（Tong et al.，2010）。由于应力状态不能超越Griffith应力状态，在这些参数的取值情况下，应力摩尔圆不可能与纵坐标轴左侧的Coulomb剪破裂线相切，表明均匀介质中正应力为负值（即处于拉张状态）的界面不可能发生剪切破裂，同时也表明位于纵坐轴左侧的Coulomb剪破裂线没有实际的物理意义。

5.2   地质体破裂活动类型的预测

分σ₃′ ≥ 0和σ₃′ <0两种情况进行讨论。

当σ₃′ ≥ 0（摩尔空间位于纵坐标轴右侧）时，所有界面在摩尔空间中极点均位于纵坐标轴（含）右侧，按照广义破裂准则，只可能发生剪切活动，不可能发生扩张活动（f_T< 0），破裂活动的类型是确定的，是剪切活动。

当σ₃′ <0（最小有效主应力为张应力），且界面在摩尔空间中极点位于纵坐标轴左侧（σ_n′ <0）时，按照广义破裂准则，界面既可能发生剪切活动（当界面的极点位于其剪切活动线（含）外侧时），也可能发生扩张活动（当界面的极点位于其扩张活动线（含）左侧时），破裂活动的类型取决于其f_S和f_T值的相对大小。当应力状态、薄弱面的方位和力学性质（扩张强度、内聚力和摩擦系数）已知时，即可实现破裂活动类型的预测。

5.3   地质体破裂活动的演化趋势分析

广义破裂活动准则中界面（各种薄弱面及方位优选的界面）的破裂活动趋势因子虽然是一个静态参数，但可以分析预测各种界面潜在的破裂活动能力及演化趋势。应用童亨茂等（2014）的方法，利用摩尔空间技术方法分别确定给定界面在Griffith应力状态下的扩张活动趋势因子和Coulomb应力状态下的剪切活动趋势因子后，从大到小顺序排列的次序即能反映各个给定界面潜在的破裂活动能力。

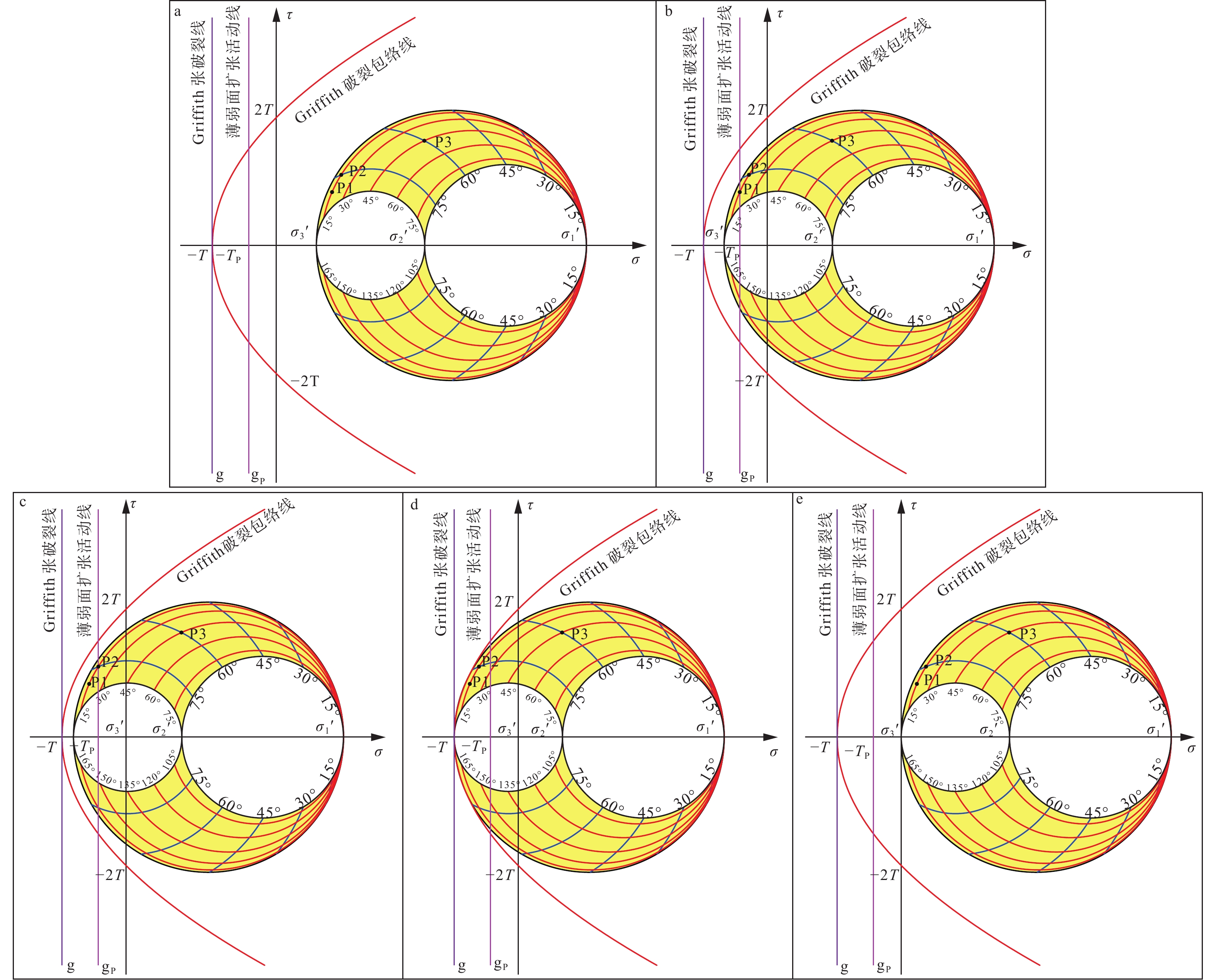
根据前面的分析，地质体产生扩张活动（包括其中的薄弱面和方位优选的界面）是由流体压力的不断增加引起的。在只考虑扩张活动的情况下，如图5所示，随着流体压力的增加，摩尔空间向左移动，f_T最大的极点P1首先接触其扩张活动线，该界面发生扩张（图5b）；随着流体压力的进一步增加，f_T较小的极点P2接触其扩张活动线，该界面发生扩张（图5c），在此过程中，P1通过界面的扩张和扩展来保持其内部的流体压力平衡（即流体压力保持不变）。而当流体压力继续增大使得区域应力状态达到Griffith应力状态时（图5d），地质体产生垂直于最小主应力轴的扩张破裂，之后便产生应力降（其值为岩石的抗张强度T），使区域应力达到新的稳定状态，摩尔空间向右移到与纵坐标轴相切的位置（图5e）。此后，薄弱面的扩张活动停止，若继续有流体补充，垂直于最小主应力轴的扩张破裂会通过扩张和扩展来保持流体压力平衡，直到流体压力补充结束。而在整个过程中，f_T最小的极点P3始终无法接触到其扩张活动线，因此该界面一直保持稳定。同样，为方便表述，简单认为极点P1、P2、P3的扩张强度T_P相等，它们的扩张活动线重合。

图  5  含多个薄弱面地质体在流体压力不断增大过程中扩张活动演化的摩尔空间图解

T—岩石的抗张强度；2T—岩石的内聚力；T_P—薄弱面的扩张强度；g—Griffith张破裂线；g_P—薄弱面的扩张活动线a—初始应力状态下的摩尔空间图解；b—极点P1与扩张活动线接触应力状态下的摩尔空间图解；c—极点P2与扩张活动线接触应力状态下的摩尔空间图解；d—Griffith应力状态下的摩尔空间图解；e—应力降后区域应力状态下的摩尔空间图解

Figure  5.  Mohr space diagram of the evolution of extension activities in geological bodies with multiple weak surfaces in the process of increasing fluid pressure

(a) Mohr space diagram in the initial stress state; (b) Mohr space diagram under the stress state when pole P1 touches the extension activation line; (c) Mohr space diagram under the stress state when pole P2 touches the extension activation line; (d) Mohr space diagram under Griffith stress state; (e) Mohr space diagram of regional stress state after stress drop T is the tensile strength of the rock, 2T is the cohesion of the rock, T_P is the extension strength of the weakness plane, g is the Griffith tensile fracture line, and g_P is the extension activation line of the weakness plane.

下载: 全尺寸图片 幻灯片

在只考虑剪切活动的情况下，对于有多个先存薄弱面的地质体剪切活动的递进变形过程，Tong and Yin（2011）已作了详细阐述，文中不再赘述。

在同时考虑扩张活动和剪切活动的情况下，对于有多个薄弱面的地质体，不同薄弱面在递进变形过程中的破裂活动方式可能是不同的，取决于其在摩尔空间中的极点优先与其扩张活动线还是剪切活动性接触（即其f_S和f_T值中哪个先达到1.0）。而当区域应力状态演化到Griffith应力状态或者Coulomb应力状态时，地质体最终会产生垂直于最小主应力轴的扩张破裂或者Coulomb破裂，具体会出现哪种破裂类型取决于整个摩尔空间优先与Griffith张破裂线还是Coulomb剪破裂线接触（即区域上的f_S和f_T值中哪个先达到1.0）。

从上面的分析可以看出，广义破裂活动准则可以实现对破裂活动演化过程的动态分析，突破了经典破裂准则静态分析的局限性，应用领域得到进一步拓展。

5.4   其他方面的应用

理论上，广义破裂活动准则可以应用到与破裂活动相关的各种作用的分析研究中，如：① 压裂过程中压裂液流动途径预测（童亨茂等，2021a）；② 压裂过程中形成的裂缝网络分布预测（童亨茂等，2021a）；③ 压裂过程中套管变形风险预测（童亨茂等，2021b）；④ 压裂过程中压窜风险预测（童亨茂等，2021a）；⑤ 固体矿产开采过程中的突水风险预测；⑥ 为地震和滑坡预测提供基础理论模型；⑦ 隧道（或坑道）开挖时的稳定性分析和评价；⑧ 与破裂相关的大型工程地基安全性分析和评价等。具体的分析方法不在这里一一详述。

6.   讨论

与广义剪切活动一样，广义破裂活动准则隐含了两个假设条件：① 界面是一个平面；② 计算区域内的应力场是均匀的。但这两个假设条件并不影响该准则在实际地质体中的应用。在给定的精度要求下，只要把实际地质体分割成足够小的有限单元，就能达到广义破裂活动准则的应用条件。

如自然界实际的断层面都是曲面，并非需要分割成无限小后才能看作是平面，而是综合考虑相关数据的误差情况和工作需要后，把断层面分割成若干段落后，每个段落的断面即可认为是平面，其内的应力场可以认为是均匀的，即可达到广义破裂活动准则的应用条件。这种有限分割，一方面满足了广义破裂活动准则的应用条件，另一方面可揭示断层不同段落、不同深度层次活动差异性的机理问题。

再如在岩石圈应力状态下，由于重力的作用，主应力值随深度是不断变化的，应力场必然是非均匀的。但如果只从宏观上分析断层作用，在介质是均匀的情况下，应力场也可以被看作是均匀的（Anderson，1951），Tong等（Tong and Yin，2011；Tong et al.，2014）按均匀应力场计算的砂箱内先存断层的活动趋势与模拟实验结果具有惊人的一致性，进一步支持了该认识。

此外，破裂活动一旦发生，无论是剪切活动（断层作用）还是扩张活动，破裂面附近均会产生应力降，形成局部应力场（Yin，1994；Morley et al.，2007；Gudmundsson et al.，2010；Tong et al.，2014），其中断层作用形成的局部应力场影响范围相对较大。另外，在破裂活动过程中，伴随着破裂面的不断扩展，地质体的结构也会发生变化，尤其是断层作用，还会伴随地质体的变形和变位。因此，在破裂活动过程中，局部应力场和地质体结构时刻在发生变化。在此过程中，应力和应变是紧密关联的两个方面，即应力导致应变，应变又引起应力的变化，构成了复杂的“应力−应变体系”（stress-strain system；童亨茂等，2015）。但是，目前破裂活动及其伴随的构造变形（如断层作用往往伴随褶皱变形，形成断层相关褶皱），以及在递进变形过程中，应力场的演化特征和规律研究还十分初步，是构造地质学的前沿研究课题，而广义破裂活动准则是联系“应力”和“破裂活动”的桥梁。随着观测资料（如高精度三维地震资料、GPS观测数据等）的不断精细，变形结果（构造几何特征）的可观测性和变形过程（构造的运动学过程）的可解析性不断增强，广义剪切破裂准则理论有望在递进变形过程中应力场演化这一研究领域发挥重要作用，也可为解决地震预测等重大难题提供理论支撑。

7.   结论

文章从产生破裂的物理本质出发，通过界面（薄弱面和假想界面）破裂活动趋势因子的分析，建立了界面发生破裂活动的准则。该准则从理论上可以定量判断任意介质、在任意三轴应力状态下、任意方位界面发生破裂活动的可能性及破裂活动类型（扩张活动或剪切活动），并把经典的破裂准则（Coulomb-Mohr准则和Griffith准则及Byerlee律为代表的滑动摩擦律）统一在了一起，把破裂（fracturing）扩展到破裂活动（fracturing activity），因此该准则被称之为广义破裂活动准则。

广义破裂活动准则揭示了Coulomb共轭剪破裂和Griffith张破裂方位优选的物理本质，并指出了其中存在的问题，可以定量评价不同界面破裂活动的演化趋势。

广义破裂活动准则适用于实际的地质体，在与破裂相关的资源勘探开发、灾害（如地震与滑坡）预测和防治中具有广阔的应用前景。